同步测控优化训练B卷[第一章 集合与简易逻辑(一)]
说明:本试卷分为第Ⅰ、Ⅱ卷两部分,请将第Ⅰ卷选择题的答案填入题后括号内,第Ⅱ卷可在各题后直接作答.共100分,考试时间90分钟.
第Ⅰ卷(选择题 共30分)
一、选择题(本大题共10小题,每小题3分,共30分)
1.数集{1,2,x2-3}中的x不能取的数值的集合是( )
A.{2,![]() } B.{-2,-
} B.{-2,-![]() } C.{±2,±
} C.{±2,±![]() } D.{2,-
} D.{2,-![]() }
}
本题考查集合中元素的互异性.
【解析】 (1)由x2-3≠1解得x=±2
(2)由x2-3≠2解得x≠±![]()
∴x不能取的值的集合为{±2,±![]() }
}
【答案】 C
2.若3x-1<3,化简![]() +
+![]() 的结果是( )
的结果是( )
A.6x-2 B.-6 C.6 D.2-6x
本题考查含绝对值不等式的解法及根式的化简.
【解析】 由3x-1<3,解得-![]() <x<
<x<![]()
∴![]() +
+![]() =
=![]() =
=![]()
=-(3x-4)+(3x+2)=6
【答案】 C
3.已知M={x![]() <
<![]() ,N={yy=x2},则M∩N等于( )
,N={yy=x2},则M∩N等于( )
A.![]() B.{xx>1}
B.{xx>1}
C.{xx<![]() D.{xx<0或x>1}
D.{xx<0或x>1}
本题考查集合的元素及交集运算.
【解析】 M={xx>1或x<0},N={yy≥0},两个集合都是数集,集合中的元素是数,易知M∩N={xx>1}.
【答案】 B
4.集合A={xx2-3x-10≤0,x∈Z},B={x2x2-x-6>0, x∈![]() ,则A∩B的非空真子集的个数为( )
,则A∩B的非空真子集的个数为( )
A.16 B.14 C.15 D.32
本题考查一元二次不等式的解法及求交集、子集的有关知识.
【解析】 易得A={x-2≤x≤5,x∈Z},B={xx>2或x<-![]() ,x∈Z=.
,x∈Z=.
∴A∩B={x-2≤x<-![]() 或2<x≤5,x∈Z}={-2,3,4,5}.
或2<x≤5,x∈Z}={-2,3,4,5}.
下面就是求集合{-2,3,4,5}的非空真子集的个数,我们知道,一个集合若有n个元素,则它的子集共有2n个,其中真子集有2n-1个,非空真子集有2n-2个,因此,本题答案为24-2=14个.
【答案】 B
5.若x是不等式组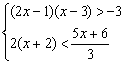 的解,则P(x+2, x-2)在( )
的解,则P(x+2, x-2)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
本题考查一元二次不等式组的解法.
【解析】 由原不等式组得![]() ,解得x<-6
,解得x<-6
∵x+2<-4,x-2<-8,
∴点P(x+2,x-2)在第三象限.
【答案】 C
6.已知集合A={-1,1},B={xmx=1},且A∪B=A,则m的值为( )
A.1 B.-1 C.1或-1 D.1或-1或0
本题考查集合间的关系及分类讨论的能力.
【解析】 由A∪B=A有B![]() A,
A,
①当m=0时,有B=![]()
![]() A
A
②当m≠0时,有B={xx=![]() }
}![]() A
A
∴![]() =1或
=1或![]() =-1,∴m=1或m=-1.
=-1,∴m=1或m=-1.
综上可知m=0或m=1或m=-1.
【答案】 D
7.已知M={xx=3k,k∈Z},P={xx=3k+1,k∈Z},Q={xx=3k-1,k∈Z},若a∈M,b∈P,c∈Q,则a+b-c∈( )
A.M B.P C.Q D.M∪P
本题考查元素与集合间关系的判定.
【解析】 设a=3k1,b=3k2+1,c=3k3-1.
则a+b-c=3(k1+k2-k3)+2=3(k1+k2-k3+1)-1,而k1+k2-k3+1∈Z.
【答案】 C
8.二次函数y=x2+(a-3)x+1的图象与x轴的两个交点的横坐标分别为x1,x2,且x1<2,x2>2,则a的取值范围是( )
A.a<1或a>5 B.a<![]()
C.a<-![]() 或a>5 D.-
或a>5 D.-
![]() <a<1
<a<1
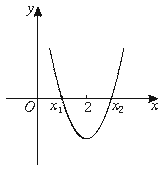 本题考查由一元二次函数的图象求参数范围的问题.
本题考查由一元二次函数的图象求参数范围的问题.
【解析】 依题意可得![]() ,
,
即![]()
解得a<![]() .
.
【答案】 B
9.设U={1,2,3,4,5},若A∩B={2},(![]() UA)∩B={4},(
UA)∩B={4},(![]() UA)∩(
UA)∩(![]() UB)={1,5},则下列结论正确的是( )
UB)={1,5},则下列结论正确的是( )
A.3![]() A且3
A且3![]() B B.3
B B.3![]() B且3∈A C.3
B且3∈A C.3![]() A且3∈B D.3∈A且3∈B
A且3∈B D.3∈A且3∈B
本题考查集合的运算.
【解析】 解答本题可利用文氏图填空的办法.
如图,∵A∩B={2},(![]() UA)∩B={4},(
UA)∩B={4},(![]() UA)∩(
UA)∩(![]() UB)={1,5}.
UB)={1,5}.
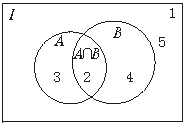
∴3必在A∩(![]() UB)中,∴3∈A,但3
UB)中,∴3∈A,但3![]() B.
B.
【答案】 B
10.若x-4+x-3>a对一切实数x恒成立,则实数a的取值范围是( )
A.(-∞,3) B.(-∞,1)
C.[1,+![]() D.(-∞,3)∪(4,+
D.(-∞,3)∪(4,+![]()
本题考查含两个绝对值符号的不等式的解法.
【解析】 【解法一】 (1)当x≥4时,x-4+x-3=(x-4)+(x-3)=2x-7≥1;
(2)当3≤x<4时,x-4+x-3=-(x-4)+(x-3)=1;
(3)当x<3时,x-4+x-3=-(x-4)-(x-3)=-2x+7>1.
综上(1)(2)(3)可知,对一切实数x,都有x-4+x-3≥1.
∴满足条件的a的取值范围为a<1.
【解法二】 如图
![]()
∵x-4+x-3=PA+PB≥1
∴满足条件的a的取值范围为a<1
【解法三】 由x-4+x-3≥(x-4)-(x+3)=1
可知满足条件的a的取值范围为a<1.
【答案】 B
第Ⅱ卷(非选择题 共70分)
 二、填空题(本大题共4小题,每小题4分,共16分)
二、填空题(本大题共4小题,每小题4分,共16分)
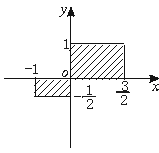
11.用描述法表示图中阴影部分的点(包括边界上的点)的坐标的集合应为_______.
本题考查平面内常用点集的表述方法.
【答案】 {(x,y)-1≤x≤![]() ,-
,-![]() ≤y≤1,xy≥0}.
≤y≤1,xy≥0}.
12.不等式![]() ≤-1的解集为_______.
≤-1的解集为_______.
本题考查分式不等式的解法.
【解析】 原不等式等价于![]() ≤0
≤0
![]()
![]() ≤0
≤0![]()
![]()
由数轴标根法可知原不等式解集为:
{x-1<x≤1或2≤x<![]() .
.
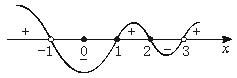
【答案】{x-1<x≤1或2≤x<![]()
13.已知集合P={xx2+(m+2)x+1=0,x∈R},若P∩{正实数}=![]() ,则实数m的取值范围为_______.
,则实数m的取值范围为_______.
本题考查集合与方程及分类讨论思想,注意在有关子集讨论中不要忽视对空集的讨论.
【解析】 (1)当P=![]() 时,有Δ=(m+2)2-4<0,解得-4<m<0.
时,有Δ=(m+2)2-4<0,解得-4<m<0.
(2)当P≠![]() 时,有
时,有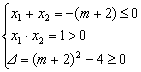
解得![]() ,得m≥0
,得m≥0
综上①②可知m>-4.
【答案】 {mm>-4}
14.已知关于x的不等式x-![]() ≤
≤![]() 的解集是单元素集A,则a=____,A=_____.
的解集是单元素集A,则a=____,A=_____.
本题考查含绝对值不等式的解法.
【解析】 由x-![]() ≤
≤![]() 解得2a≤x≤a2+1
解得2a≤x≤a2+1
又∵不等式的解集为单元素集,∴a2+1=2a,
解得a=1,此时A={2}.
【答案】 1 {2}
三、解答题(本大题共5小题,共54分.解答应写出文字说明、证明过程或演算步骤)
15.(本小题满分8分)
已知集合A={xx2-5x+6<0},B={xx2-4ax+3a2<0}且A![]() B,求实数a的取值范围.
B,求实数a的取值范围.
本题考查含参数的一元二次不等式的解法,集合的交、并运算及分类讨论的能力.
【解】 A={xx2-5x+6<![]() ={x2<x<
={x2<x<![]() ,
,
B={xx2-4ax+3a2<![]() ={x(x-a)(x-3a)<
={x(x-a)(x-3a)<![]()
(1)当a>0时,B={xa<x<3a},
∵A![]() B,∴
B,∴![]() ,解得1≤a≤2.
,解得1≤a≤2.
(2)当a<0时,B={x3a<x<a}.
由A![]() B,得
B,得![]() ,解集为
,解集为![]() .
.
(3)当a=0时,B={xx2<![]() =
=![]() 不合题意.
不合题意.
综上(1)(2)(3)可知1≤a≤2.
16.(本小题满分10分)
已知集合A={x-2<x<-1或x>1},B={xx2+ax+b≤0},且A∩B={x1<x≤3},A∪B={xx≥-2},试求a,b的值.
本题考查集合间的运算.
这样的定集合与动集合之间的运算通常是利用数轴进行子、交、并、补的运算,也就是简单的数形结合问题.
【解】 如图,可知B={x-1≤x≤3}.
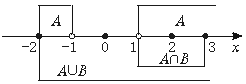
即-1≤x≤3是不等式x2+ax+b≤0的解集.
∴![]() ,解得
,解得![]() .
.
17.(本小题满分12分)
已知集合A={xx2-4x+3<0},B={xx-3≤1}.
(1)试定义一种新的集合运算Δ,使AΔB={x1<x<2};
(2)按(1)的运算,求出BΔA.
本题考查学生对集合交、并、补集定义的理解及相关知识的联系与迁移能力,培养学生的发散性思维和创造性思维.
【解】 易得A={x1<x<3},B={x2≤x≤4}.
(1)∵AΔB={x1<x<![]() ,
,
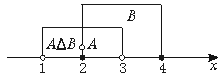
由图可知AΔB中的元素都在A中但不在B中,
∴定义AΔB={xx∈A且x![]() B}.
B}.
(2)由(1)可知BΔA={xx∈B且x![]() A}={x3≤x≤4}.
A}={x3≤x≤4}.
18.(本小题满分12分)
已知集合A={x-x2+x+2<0},B={x2x2+(2k+5)x+5k<0,k∈R}.求A∩B;
本题考查含参数不等式的解法及利用数轴求集合的子集.
【解】 A={xx>2或x<-![]() ,B={x(x+
,B={x(x+![]() )(x+k)<
)(x+k)<![]() .
.
①当k>![]() 时,B={x-k<x<-
时,B={x-k<x<-![]() .
.
由图(1)可知A∩B={x-k<x<-![]() .
.
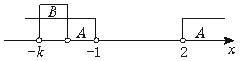
图(1)
②当k=![]() 时,B=
时,B=![]() ,A∩B=
,A∩B=![]() .
.
③当k<![]() 时,B={x-
时,B={x-![]() <x<-
<x<-![]() .
.
(i)当-![]() <-k≤-1即1≤k<
<-k≤-1即1≤k<![]() 时,
时,
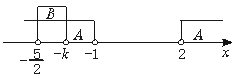
图(2)
由图(2)可知A∩B={x-![]() <x<-k}
<x<-k}
(ii)当-1<-k≤2即-2≤k<1时,
由图(3)知A∩B={x-![]() <x<-
<x<-![]() .
.
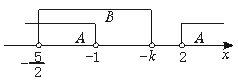
图(3)
(iii)当-k>2即k<-2时,
由图(4)可知A∩B={x-![]() <x<-1或2<x<-
<x<-1或2<x<-![]() .
.
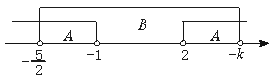
图(4)
19.(本小题满分12分)
汽车在行驶中,由于惯性作用,刹车后还要继续向前滑引一段距离才能停住,我们将这段距离称为“刹车距离”.刹车距离是分析事故的一个重要因素,在一个限速为40千米/时以内的弯道上,甲乙两辆车相向而行,发现情况不对,同时刹车,但还是相碰了,事后现场测得甲车的刹车距离超过了12米,乙车的刹车距离超过了10米,已知甲乙两种车型的刹车距离S(米)与车速x(千米/时)之间有如下关系:
S甲=0.1x+0.01x2,S乙=0.05x+0.005x2
问两车相碰的主要责任是谁?
本题考查学生解应用题及不等式的能力.
【解】 由题意知,对于甲车:
0.1x+0.01x2>12![]() x2+10x-1200>0
x2+10x-1200>0![]() x>30或x<-40(舍去)
x>30或x<-40(舍去)
根据题意,甲车刹车距离略超过12米
∴甲车速不会超过30千米/时很多;
对于乙车:0.05x+0.005x2>10![]() x2+10x-2000>0
x2+10x-2000>0
![]() x>40或x<-50(舍去)
x>40或x<-50(舍去)
∵乙车速已经大于弯道限速40千米/时,
∴主要责任在乙.