第二十一教时
教材：解斜三角形的应用，课本《实习作业》《教学与测试》78、79课
目的：要求学生能灵活运用正弦定理和余弦定理解斜三角形，进一步培养学生把实际问题转化为数学问题，用数学方法解决实际问题的能力。
过程：一、《教学与测试》P163 第78课
例一
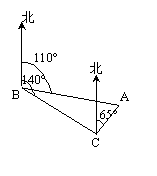
如图，货轮在海上以40km/h的速度沿40°方位角航行，为了确定船位，船在B点观察A的方位角为110°，航行半小时后到达C点，观察A的方位角为65°，则货轮到达C点时与灯塔A的距离是多少？
解：在△ABC中，
°
ÐACB=(180° - 40°)+65°=105°
∴ ÐA=180° - (30°+105°)=45°
由正弦定理：
答：从略
例二 如图所示，有两条相交成60°角的直路
交点是O，甲、乙分别在
上，起初甲离O点3km，乙离O点1km，后来两人同时用每小时4km的速度，甲沿
的方向，乙沿
的方向步行
1．起初两人的距离是多少？
2．用包含t的式子表示t小时后两人的距离
3．什么时候两人的距离最短？
解：1．设甲、乙两人最初的位置是A、B
则
2=
2+
2-2cos60°=
∴=
2．设甲、乙两人t小时后的位置分别为P，Q则
=4t,
=4t
当
时
2=
当
时2=
上面的式子是一致的，∴2=
即：=
3．∵2=
当
时 即15分钟末PQ最短，最短距离为2km
二、课本P135 5—11 《实习作业》
例一、例二 提出问题，讲测量的过程及理由，最后计算
三、补充
例一 如图，如果三个力平衡
，并且
和
, 
和, 和
的夹角分别是a,b,g, 1．求证：
2．如果
, b=150°, g=90°
求
和
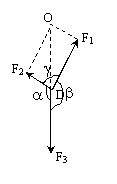证：∵三个力平衡
∴以
, 
为边的平行四边形
对角线
=
在△
中, 
= Ð
=180°-b
Ð=180°-g
Ð
=180°-a
由正弦定理：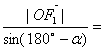
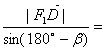
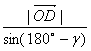
即：
四、作业：《教学与测试》P164 练习题