高一数学期终试卷
一、选择题：
1、已知集合
，则集合
的元素个数为
（ ）
A、10 B、9 C、8 D、7
2、已知甲：点
在第二象限，乙：
，则A是B 的
（ ）
A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既非充分又非必要条件
3、已知函数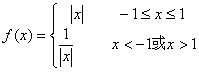
，那么
（ ）
A、
B、4
C、1
D、均不正确
4、若
，则
（ ）
A、
B、
C、
D、
5、函数
的的单调增区间为
（ ）
A、
B、
C、
D、
6、已知全集
，
，
，则
等于
（ ）
A、
B、
C、
D、
7、
为等比数列且
，则公比
的值为
（ ）
A、
B、
C、
D、
8、若
，则
为
（ ）
A、
B、
C、
D、
9、不等式
的解集为
，其中
，那么
的解集为
（ ）
A、
B、
C、
D、
10、等比数列的各项都是正数，且
，则
的值是
（ ）
A、20 B、10 C、5 D、40
11、方程
至少有一个负根的充要条件
（ ）
A、
B、
C、
D、
12、函数
，使
成立的的值的集合为 （ ）
A、是
B、有且只有一个元素 C、有且只有二个元素 D、有无数个元素
一、填空题：
13、
函数
的定义域为
14、已知是等差数列，公差
，且
成等比数列，则
15、不等式
的解集非空，则
的取值范围为
16、
数
与函数
互为反函数，则
二、解答题：
17、集合
，
，
，
，求实数
的值。
18、(1)解不等式：
(2)求和：
19、已知数列｛an｝是等差数列，且a23=49,a32=67.
(Ⅰ)求数列｛an｝的通项公式an；
（Ⅱ）该数列在20至50之间共有多少项？求出这些项的和.
20、函数
对一切
均有
成立，且
，
（1）求
（2）当
恒成立时，求实数的取值范围
|
21、（14分）对于任意函数f（x）定义域为D，如图构造一个数列发生器，其工作原理如下：
①输入初始数据
，输出
②若
，则机器自动停止；若
，则数据x1反馈回输入端，再输出
，依次继续下去。设
。
问（1）若输入一个初始数据x0，使得机器运行一步后即停止工作，求x0的取值范围；
（2）若输入一个初始数据x0，使得机器能产生一个无穷的常数数列，求x0的值；
（3）若输入一个初始数据x0，使得机器能产生一个无穷的递增数列，求x0取值范围。
22、已知
（1）求的反函数
（2）若不等式
对
上的每一个的值都成立，求实数
的取值范围
答案
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | A | A | B | A | B | C | C | B | A | C | C |
13、
；14、
；15、
；16、 
17、解：由题意得
，要使，
只能
，
，
是方程
的两根
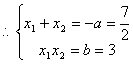
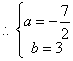
18、（1）解：
18、（2）解：
是以
为首项，
为公比的等比数列，共
项
（1）当
，即
时 
（2）当
，即
时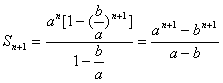 
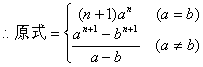
19、（Ⅰ）d=2 an=2n+3
（Ⅱ）依条件得20＜2n+3＜50,∵n∈N°,
∴n=9，10，11，…，23，∴共有 23-8=5项
这些项的和为 S23-S8=525.（或求出a9=21,再求和）
20、解：（1）取
，
，得
又
（2）
，
要使恒成立，必须且只需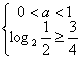
21、解：（1）由已知
且
，即
且；∴
（2）机器产生一个无穷的常数数列，即
对
恒成立，
∴
即
，又，
（3）由
， 恒成立，则机器能产生一个无穷的递增数列,
由
，得x0＞3或x0＜-1，又，∴x0＞3
∴x0＞3时机器能产生一个无穷的递增数列
22、解：（1）
，当
时，
，即原函数的值域为
由
得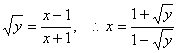
（2）
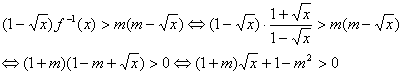
令
，
原不等式对一切
恒成立等价于
对一切
恒成立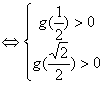
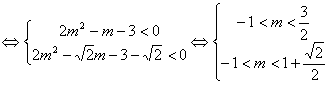
