高一数学上学期期中试卷3
一、选择题
1.已知M={x︱x![]() <9}a=-4,则(
)
<9}a=-4,则(
)
A.a![]() M
B.a
M
B.a![]() M
C.{a}
M
C.{a}![]() M
D.{a}
M
D.{a}![]() M
M
2.设集合A和B都是整数集N*,映射f:A→B 把集合A中的元素,n映射到集合B中的元素是2![]() +n,则在映射f 下,象20的原象是(
)
+n,则在映射f 下,象20的原象是(
)
A.3 B。2 C。5 D。4
3.把下列语句看成复合命题时,是“p或q”形成且为真命题的是( )
A.3和15都是15的倍数 B。5≥0
C.1+![]() 不是实数
D。四边形ABCD是平行四边形或梯形
不是实数
D。四边形ABCD是平行四边形或梯形
4.已知不等式︱x-a︱<b的解集是{x︱-3<x<9}则a、b的值分别为( )
A.-3,9 B。3,6 C。3,9 D。-3,6
5.若函数y=(2k+1)x+b在家(-![]() ,+
,+![]() )上为减函数,则(
)
)上为减函数,则(
)
A.k<-![]() B.k<
B.k<![]() C.k>-
C.k>-![]() D.k>
D.k>![]()
6.a、b为实数,“a+b≠0”的一个必要但不充分条件是( )
A.ab>0 B.a>0且b>0
C.a+b>3 D. a≠0或b≠0
7.已知偶函数y=f(x)在[0, ![]() ]上是增函数,则( )
]上是增函数,则( )
A.f(-![]() )<f(
)<f(![]() )<f(-2)
B. f(
)<f(-2)
B. f(![]() )<f(-2)< f(-
)<f(-2)< f(-![]() )
)
C. f(-2)< f(-![]() )<f(
)<f(![]() )
D. f(-2)< f(
)
D. f(-2)< f(![]() )<f(-
)<f(-![]() )
)
8.函数y=-![]() (-1≤x<0)的反函数是(
)
(-1≤x<0)的反函数是(
)
A.y=![]() (0≤x≤1)
B. y=
(0≤x≤1)
B. y=![]() (-1≤x≤0)
(-1≤x≤0)
C. y=-![]() (-1<x≤0)
D. y=-
(-1<x≤0)
D. y=-![]() (0≤x≤1)
(0≤x≤1)
![]()
![]() 9. x
9. x![]() >3
x
>3
x![]() +x
+x![]() >6
>6
是 的 ( )
x![]() >3
x
>3
x![]() x
x![]() >9
>9
A.充分不必要条件 B。必要不充分条件
C.充要条件 D。既不充分也不必要条件
10.条件甲:不等式ax![]() +2ax+1>0的解集为R,条件乙:0<a<1,则条件甲是条件乙的( )
+2ax+1>0的解集为R,条件乙:0<a<1,则条件甲是条件乙的( )
A.必要而不充分条件 B。充分而不必要条件
C.充要条件 D。既非充分又非必要条件
11.函数y=![]() 的定义域为(
)
的定义域为(
)
A.(-![]() ,0)
,0)![]() (0,+
(0,+![]() )
B。(-
)
B。(-![]() ,-1)
,-1)![]() (-1,0)
(-1,0)
C.(-![]() ,0)
,0)![]() (0,1)
(0,1)![]() (1,+
(1,+![]() )
D。(-
)
D。(-![]() ,0)
,0)
12.若点(a,b)在函数y=f(x)的图象上,则下列各点中必在其反函数图象上的是( )
A.P![]() (a,f
(a,f![]() (a))
B.P
(a))
B.P![]() (f
(f![]() (b),b)
(b),b)
C.P![]() (b,f
(b,f![]() (b))
D.P
(b))
D.P![]() (f
(f![]() (a),a)
(a),a)
二、填空题
13.不等工(4-m)x![]() -3x+m+4>0的解集为R,m可取的正整数的个数是_______________
-3x+m+4>0的解集为R,m可取的正整数的个数是_______________
![]() 3 (x=1)
3 (x=1)
14.设f(x)=2x+1 , g(x)= ,则g(4)=__________________
f[g(x-1)] ( x≥2)
15.若f(x)=![]() (x-1)
(x-1) ![]() +a的定义域和值域都是[1,b],则a=____________,b=________
+a的定义域和值域都是[1,b],则a=____________,b=________
16.含有三个实数的集合可表示为{a,![]() ,1}也可表示为{a
,1}也可表示为{a![]() ,a+b,0}则a
,a+b,0}则a![]() +b
+b![]() 的值为_____________________
的值为_____________________
三、解答题
17.集合M={x︱︱x-1︱<1},N={x︱x![]() +2x-3>0}
+2x-3>0}
求:(1)M![]() N (2)M
N (2)M![]() N
N
18.已知f(x)=log![]()
![]() ·log
·log![]() (3x),若x
(3x),若x![]() [
[![]() ,27],求f(x)的最大值和最小值。
,27],求f(x)的最大值和最小值。
19.已知f(x)=-![]() x
x![]() +x,问:是否存在实数m、n,函数的定义域是[m,n]时,其值域是[2m,2n]?
+x,问:是否存在实数m、n,函数的定义域是[m,n]时,其值域是[2m,2n]?
20.已知一个三角形的两边是方x![]() +px+2=0的两根,第三边长为3,求p的取值范围。
+px+2=0的两根,第三边长为3,求p的取值范围。
21.已知:f(x) ![]() +c,且f[f(x)]=f(x
+c,且f[f(x)]=f(x![]() +1),c为常数。
+1),c为常数。
(1) 设g(x)= f[f(x)],求g(x)的解析式
(2) 记f(x)=g(x)-![]() f(x),试问是否存在实数
f(x),试问是否存在实数![]() ,使得f(x)在区间(-
,使得f(x)在区间(-![]() ,-
,-![]() )上是减函数,并且在区间(-
)上是减函数,并且在区间(-![]() ,0)上是增函数?
,0)上是增函数?
22.函数f(x)log![]() (1-x),g(x)=log
(1-x),g(x)=log![]() (1+x)(a>0,且a≠1)
(1+x)(a>0,且a≠1)
(1) 讨论函数f(x)= f(x)-g(x)的奇偶性;
(2) 关于x的方程a![]() =a
=a![]() -x有两个不等的实根,试求m的取值范围。
-x有两个不等的实根,试求m的取值范围。
答案:
1 .B 2。D 3。B 4。B 5。A
6 .D 7。B 8。C 9。A 10。A
11 .D 12。C
13.m≠4,∴4-m>0,且△=9-4(4-m)(m+4)<0,即m<4,且m![]() <
<![]() ,∴-
,∴-![]() <m<4,取m=1,2,3共3个。
<m<4,取m=1,2,3共3个。
14.G(4)=f[g(4-1)]=f[f(3)]=f{f[g(3-1)]}=f{f[g(2)]}=f{f[g(1)]}=f{f(7)}=f(15)=31
15.f(x)在x≥1时,单调递增,∴f(1)=1,f(b)=b,即a=1, ![]() (b-1)
(b-1)![]() +1=b,∴b=3,填a=1,b=3
+1=b,∴b=3,填a=1,b=3
16.∵a≠0∴b=0,∴a![]() =1,∴a=±1,但a≠1,∴a=-1,∴a
=1,∴a=±1,但a≠1,∴a=-1,∴a![]() =-1
=-1
17.由︱x-1︱<1,得0<x<2,即M={x︱0<x<2},由x![]() +2x-3>0,得N={x︱x<-3,或x>1},∴(1)M
+2x-3>0,得N={x︱x<-3,或x>1},∴(1)M![]() N={x︱1<x<2},(2)M
N={x︱1<x<2},(2)M![]() N={x︱x<-3,或x>0}
N={x︱x<-3,或x>0}
18.f(x)=(log![]() x-log
x-log![]() 27)(log
27)(log![]() x+log
x+log![]() 3)
3)
=(log![]() x-3) (log
x-3) (log![]() x+1)=log
x+1)=log![]() x-2log
x-2log![]() x-3=(log
x-3=(log![]() x-1)
x-1)![]() -4
-4
由x![]() [
[![]() ,27],∴-2<log
,27],∴-2<log![]() x<3,当log
x<3,当log![]() x=1,即x=3时,f(x)有最小值-4;当log
x=1,即x=3时,f(x)有最小值-4;当log![]() x=-2,即x=
x=-2,即x=![]() 时,f(x)有最大值9-4=5
时,f(x)有最大值9-4=5
19.解:∵f(x)=- ![]() x
x![]() +x的对称轴为x=1.当m≤n≤1时,值域为[f(m),f(n)],∵f(m)=2m,f(n)=2n.即2m=-
+x的对称轴为x=1.当m≤n≤1时,值域为[f(m),f(n)],∵f(m)=2m,f(n)=2n.即2m=-![]() m
m![]() +m,2n=-
+m,2n=-![]() n
n![]() .解得m=-2,n=0当1≤m≤n时,值域为[f(n),f(m)]
.解得m=-2,n=0当1≤m≤n时,值域为[f(n),f(m)]
∴f(n)=2m,f(m)=2n,即2n=-![]() m
m![]() +m,2m=-
+m,2m=-![]() n
n![]() +n,而-
+n,而-![]() m
m![]() +m≤-
+m≤-![]() +1=
+1=![]() ,∴n≤
,∴n≤![]() 与n>1矛盾。故意此时无解。当1
与n>1矛盾。故意此时无解。当1![]() [m,n]时,有f(1)=2n,此时n=
[m,n]时,有f(1)=2n,此时n=![]() ,与n>1矛盾,此时亦无解。
,与n>1矛盾,此时亦无解。
∴存在唯一的实数m=-2,n=0满足条件。
![]()
![]() △=p
△=p![]() -8≥0 ︱a-b︱<3
-8≥0 ︱a-b︱<3
20.解:设a,b为三角形的两边。∵ a+b=-p 且
有-![]() <p<-3
<p<-3
ab=2 a+b>3
21.解:(1)f[f(x)]=x![]() +2cx
+2cx![]() +c
+c![]() +c, f(x
+c, f(x![]() +1)=x
+1)=x![]() +2x
+2x![]() ,
,
∴c=1, ∴g(x)=x![]() +2x
+2x![]() +1
+1
(2)f(x)=g(x)-![]() f(x)=x
f(x)=x![]() +(2-
+(2-![]() )x
)x![]() +2-
+2-![]()
假设存在实数![]() 满足条件,则任取x
满足条件,则任取x![]() <x
<x![]() <0, 有-x
<0, 有-x![]() >-x
>-x![]() , x
, x![]() >x
>x![]()
 f(x
f(x![]() )-f( x
)-f( x![]() )=( x
)=( x![]() -x
-x![]() )( x
)( x![]() +x
+x![]() +2-
+2-![]() )
)
①
当x![]() ,x
,x![]()
![]() (-
(-![]() ,-
,-![]() )时,∵f(x
)时,∵f(x![]() )- f( x
)- f( x![]() )>0
)>0
则x![]() +x
+x![]() +2-
+2-![]() >0而x
>0而x![]() +x
+x![]() >
>![]() +
+![]() =1,∴
=1,∴![]() ≤3
≤3
②当x![]() ,x
,x![]()
![]() (-
(-![]() ,0)时,∵f(x)单调递增, f(x
,0)时,∵f(x)单调递增, f(x![]() )- f( x
)- f( x![]() )<0
)<0
则x![]() +x
+x![]() +2-
+2-![]() <0,而x
<0,而x![]() +x
+x![]() <
<![]() +
+![]() =1,∴
=1,∴![]() ≥3综上述有
≥3综上述有![]() =3满足条件。
=3满足条件。
22.解:(Ⅰ)∵f(x)=log![]() (1-x),g(x)= log
(1-x),g(x)= log![]() (1+x)而f(x)=f(x)-g(x)
(1+x)而f(x)=f(x)-g(x)
∴1-x>0且1+x>0 ∴-1<x<1,而f(x)的定义域为(-1,1)
f(-x)=f(-x)-g(-x) =log![]() (1+x)- log
(1+x)- log![]() (1-x)
(1-x)
=-[f(x)-g(x)]=-f(x)
(Ⅱ)由a![]() =a
=a![]() =2+x-x
=2+x-x![]() >0
>0
a![]() =a
=a![]() =1-m>0
=1-m>0
∴-1<x<2且m<1
∴原方程即为
x![]() -2x-1=m(-1<x<2,m<1)
-2x-1=m(-1<x<2,m<1)
方法(一)令y![]() =x
=x![]() -2x-1, y
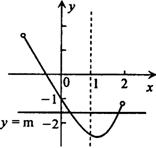
-2x-1, y![]() =m ,在同一坐标中画出它们的图象,则方程有两根时,-2<m<-1
=m ,在同一坐标中画出它们的图象,则方程有两根时,-2<m<-1
方法(二)令G(x)=x![]() -2x-m-1,原方程有两根等价于G(x)的图象在(-1,2)内与x 轴有两个不交点,2)内与x轴有两个不同交点。
-2x-m-1,原方程有两根等价于G(x)的图象在(-1,2)内与x 轴有两个不交点,2)内与x轴有两个不同交点。
∴G(-1)>0且G(2)>0且△>0=-2<m<-1