高一数学试题
一、选择题（本大题共12小题，每小题5分，共60分）
1、满足
的所有集合A的个数
（ ）
A、1个 B、2个 C、3个 D、4个
2、下列各个对应中,构成映射的是 ( )
A B A B A B A B
 |
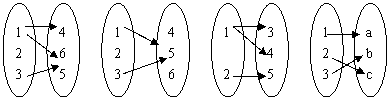A B C D
3. 下列各式中正确运用对数运算性质的是 （）
A. 
B. 
C. 
D. 
4、
的定义域是 （ ）
A 、
B、
C、
D 、
5.一个扇形OAB的面积是1cm2,它的周长是4cm,则它的中心角是 [ ]
A.2弧度 B.3弧度 C.4弧度
D.5弧度
6、设偶函数f(x)的定义域为R，当
时，f(x)是减函数，
则f(-2),f(
),f(-3)的大小关系是
（ ）
A、f()>f(-3)>f(-2)
B、f()>f(-2)>f(-3)
C、f()<f(-3)<f(-2)
D、f()<f(-2)<f(-3)
（ ）
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8、有以下四组角：(1)kπ+
；(2)kπ--；(3)2kπ±；(4)--kπ+ (k∈z)其中终边相同的是（ ）
A、(1)和(2) B、(1)、(2)和(3) C、(1)、(2)和(4) D、(1)、(2)、(3)和(4)
9、下列五个命题中，正确的有几个？ （ ）
① 函数
与
是同一函数；②若集合
中只有一个元素，则
；③ 函数
是奇函数；④函数
在
上是增函数；
⑤定义在R上的奇函数
有
A、1 B、2 C、3 D、4
10、已知集合
，
，且
，若
=A，则 （ ）
A、－3≤
≤4 B、－3
4
C、
D、
≤4
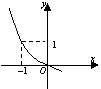11、定义在R上的函数
的图象如图所示，它在定义域上
是减函数，给出如下命题：①
=1；②
；③若
，则
；④若
，则
，其中正确的是 （ ）
A、②③ B、①④ C、②④ D、①③
12、100名学生报名参加A、B两个课外活动小组，报名参加A组的人数是全体学生人数的
，报名参加B组的人数比报名参加A组的人数多3，两组都没报名的人数是同时报名参加A、B两组人数的
多1，求同时报名参加A、B两组人数
（ ）
A、36 B、13 C、24 D、27
二、填空题（本题共4小题，每小题4分，共16分）
13、已知
的真子集的个数是
。
14. 若
,B={
,C={
,
则
.
15、 函数
,当
时是增函数，则
的取值范围是
。
16、已知tanα=3 则
的值为________
三、解答题
17.求函数y= 
+1g(2sinx+
)的定义域.
18．已知≤
≤1，若函数
在区间[1，3]上的最大值为
，最小值为
，令
．
（1）求
的函数表达式；
（2）判断函数在区间[1/3，1]上的单调性，并求出的最小值 .
19．若是定义在
上的增函数，且
⑴求
的值；⑵若
，解不等式
21、季节性服装当季节即将来临时，价格呈上升趋势，设某服装开始时定价为10元，并且每周(7天)涨价2元，5周后开始保持20元的价格平稳销售；10周后当季节即将过去时，平均每周削价2元，直到16周末，该服装已不再销售。
（1）试建立价格P与周次t之间的函数关系式。
（2）若此服装每件进价Q与周次t之间的关系为Q＝－0.125(t－8)2＋12，t∈[0，16]，t∈N*，试问该服装第几周每件销售利润L最大? （注：每件销售利润＝售价－进价）
22、已知二次函数的二次项系数为，且不等式
的解集为（1 ，3），
（1）
如果方程
有两个相等的根，求的解析式；
（2）
若果函数的最大值为正数，求的取值范围。