高一数学同步测试（1）—集合的概念与运算
一、选择题：
1．集合
的子集个数是 （ ）
A．32 B．31 C．16 D．15
2．如果集合A={xax2＋2x＋1=0}中只有一个元素，则a的值是 （ ）
A．0 B．0 或1 C．1 D．不能确定
3．设集合
，
其中
，则下列关系中正确的是（ ）
A．
M B．
C．
D．
4．设集合A={x1＜x＜2}，B={xx＜a}满足A≠B，则实数a的取值范围是 （ ）
A．
B．
C．
D．
5．满足{1，2，3}
M {1，2，3，4，5，6}的集合M的个数是 （ ）
A．8 B．7 C．6 D．5
6．设全集I={0，1，2，3，4}，集合A={0，1，2，3}，集合B={2，3，4}，则
∪
= （ ）
A．{0} B．{0，1} C．{0，1，4} D．{0，1，2，3，4}
7．集合A={a2，a＋1，-1}，B={2a－1， a－2 ， 3a2＋4}，A∩B={-1}，则a的值是（ ）
A．－1 B．0 或1 C．2 D．0
8．已知集合M={(x，y)4x＋y=6}，P={(x，y)3x＋2y=7}，则M∩P等于 （ ）
A．(1，2) B．{1}∪{2} C．{1，2} D．{(1，2)}
9．设集合A={xx∈Z且－10≤x≤－1}，B={xx∈Z且x≤5 }，则A∪B中元素的个数为 （ ）
A．11 B．10 C．16 D．15
10．已知全集I＝N，集合A＝{xx＝2n，n∈N}，B＝{xx＝4n，n∈N}，则 （ ）
A．I＝A∪B B．I＝∪B C．I＝A∪
D．I＝∪
|
，则 （ ）
A．M =N B．
C．
D．∩
12．集合A={xx=2n＋1，n∈Z}， B={yy=4k±1，k∈Z}，则A与B的关系为 （ ）
A．AB B．A 
B C．A=B
D．A≠B
二、填空题：
13．设集合U={(x，y)y=3x－1}，A={(x，y)
=3}，则
A=
.
14．集合M={a 
∈N，且a∈Z}，用列举法表示集合M=_____
___．
15．设含有10个元素的集合的全部子集数为S，其中由3个元素组成的子集数为T，则T/S的值为 .
16．设A={xx2＋x－6=0}，B={xmx＋1=0}，且A∪B=A，则m的取值范围是 .
三、解答题：
17．已知集合A＝｛x｜－1＜x＜3
，A∩B＝
，A∪B＝R，求集合B．
18．已知集合A={x1≤x＜4}，B={xx＜a};若A
B，求实数a的取值集合．
19．已知集合A={－3，4}，B={xx2－2px＋q=0}，B≠φ，且B
A，求实数p，q的值．
20．设集合A={xx2＋4x=0}，B={xx2＋2(a＋1)x＋a2－1=0} ，A∩B=B， 求实数a的值．
21．已知集合A＝｛x∈R｜x2－2x－8＝0｝，B＝｛x∈R｜x2＋ax＋a2－12＝0｝，BA，求实数a的取值集合．
22．集合A＝｛x｜x2－ax＋a2－19＝0｝，B＝｛x｜x2－5x＋6＝0｝，C＝｛x｜x2＋2x－8＝0｝．
（1）若A∩B＝A∪B，求a的值；
（2）若A∩B，A∩C＝，求a的值．
参考答案
一、选择题：ABDAC CDDCC BC
二、填空题：13.{(1，2)}，14.
，15.15/128 ，16.
．
三、解答题：
17.解析：由A∩B＝及A∪B＝R知全集为R，
RA＝B，
故B＝RA＝｛x｜x≤－1或x≥3｝．
18.解析： 将数集A表示在数轴上(如图)，要满足AB，表示数a的点必须在4或4的右边，所求a的取值集合为{aa≥4}.
19.解析：若B=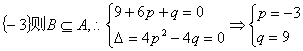
若B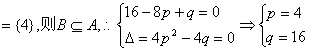
，
若B={－3，4}则
则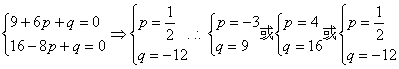
20.解析：A={0，－4} 又
(1)若B=
，则
，
(2)若B={0}，把x=0代入方程得a=
当a=1时，B=
(3)若B={－4}时，把x=－4代入得a=1或a=7.
当a=1时，B={0，－4}≠{－4}，∴a≠1.
当a=7时，B={－4，－12}≠{－4}， ∴a≠7.
(4)若B={0，－4}，则a=1 ，当a=1时，B={0，－4}， ∴a=1
综上所述：a
21.解析： A＝｛－2，4｝，∵BA，∴B＝，｛－2｝，｛4｝，｛－2，4｝
若B＝，则a2－4(a2－12)＜0，a2＞16，a＞4或a＜－4
若B＝｛－2｝，则(－2)2－2a＋a2－12＝0且Δ=a2－4(a2－12)=0，解得a=4.
若B＝｛4｝，则42＋4a＋a2－12＝0且Δ=a2－4(a2－12)=0，此时a无解；
若B＝｛－2，4｝，则
∴a＝－2
综上知，所求实数a的集合为｛a｜a＜－4或a＝－2或a≥4｝.
22.解析： 由已知，得B＝｛2，3｝，C＝｛2，－4｝.
(1)∵A∩B＝A∪B，∴A＝B
于是2，3是一元二次方程x2－ax＋a2－19＝0的两个根，由韦达定理知：
解之得a＝5.
(2)由A∩B 
∩
，又A∩C＝，得3∈A，2
A，－4A，由3∈A，
得32－3a＋a2－19＝0，解得a＝5或a=－2
当a=5时，A＝｛x｜x2－5x＋6＝0｝＝｛2，3｝，与2A矛盾；
当a=－2时，A＝｛x｜x2＋2x－15＝0｝＝｛3，－5｝，符合题意.
∴a＝－2.