高一数学同步测试(2)—不等式的解法
一、选择题:
1.不等式1≤|x-3|≤6的解集是 ( )
A.{x|-3≤x≤2或4≤x≤9} B.{x|-3≤x≤9}
C.{x|-1≤x≤2} D.{x|4≤x≤9}
2.已知集合A={xx-1<2},B={xx-1>1},则A∩B等于 ( )
A.{x-1<x<3} B.{xx<0或x>3}
C.{x-1<x<0} D.{x-1<x<0或2<x<3}
3.不等式2x-1<2-3x的解集为 ( )
A.{xx<![]() 或x>1} B.{xx<
或x>1} B.{xx< ![]() }
}
C.{xx<![]() 或
或 ![]() <x<
<x< ![]() } D.{x-3<x<
} D.{x-3<x<![]() }
}
4.已知集合A={xx+2≥5},B={x-x2+6x-5>0},则A∪B等于 ( )
A.R B.{xx≤-7或x≥3}
C.{xx≤-7或x>1} D.{x3≤x<5}
5.不等式![]() 的整数解的个数是 ( )
的整数解的个数是 ( )
A.7 B.6
C.5 D.4
6.不等式![]() 的解集是 ( )
的解集是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
7.已知集合A={xx-1<2},B={xx-1>1},则A∩B等于 ( )
A.{x-1<x<3} B.{xx<0或x>3}
C.{x-1<x<0} D.{x-1<x<0或2<x<3}
8.己知关于x的方程(m+3)x2-4mx+2m-1=0的两根异号,且负根的绝对值比正根大,那么实数m的取值范围是 ( )
A.-3<m<0 B.m<-3或m>0
C.0<m<3 D.m<0 或 m>3
9.设集合![]() ,则能使P∩Q=φ成立的
,则能使P∩Q=φ成立的![]() 的值是( )
的值是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
10.已知![]() ,若不等式
,若不等式![]() 在实数集
在实数集![]() 上的解集不是空集,则
上的解集不是空集,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
11.已知集合A={x|x2-x-6≤0},B={x|x2+x-6>0},S=R,则![]() (A∩B)等于( )
(A∩B)等于( )
A.{x|-2≤x≤3} B.{x|2<x≤3![]()
C.{x|x≥3或x<2![]() D.{x|x>3或x≤2}
D.{x|x>3或x≤2}
12.设集合![]() ,若
,若![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
二、填空题:
13.已知集合A={xx+2≥5},B={x-x2+6x-5>0},则A∪B= ;
14.若不等式2x-1>m(x2-1)对满足-2≤x ≤2 的所有实数m都成立,则实数x的取值范围是 .
15.不等式0≤x2+m x+5≤3恰好有一个实数解,则实数m的取值范围是 .
16.己知关于x的方程(m+3)x2-4mx+2m-1=0 的两根异号,且负根的绝对值比正根大,那么实数m的取值范围是 .
三、解答题:
17.解下列不等式:
⑴x+2>x+2; ⑵3≤x-2<9.
18.解关于![]() 的不等式:(1) x2-(a+1)x+a<0,(2)
的不等式:(1) x2-(a+1)x+a<0,(2) ![]() .
.
19.设集合A={xx2+3k2≥2k(2x-1)},B={xx2-(2x-1)k+k2≥0},且A![]() B,试求k的取值范围.
B,试求k的取值范围.
20.不等式(m2-2m-3)x2-(m-3)x-1<0的解集为R,求实数m的取值范围.
21.已知二次函数y=x2+px+q,当y<0时,有-![]() <x<
<x<![]() ,解关于x的不等式
,解关于x的不等式
qx2+px+1>0.
22.若不等式![]() 的解集为
的解集为![]() ,求实数p与q的值.
,求实数p与q的值.
参考答案
一、选择题: ADBCA BDABB DA
二、填空题:
13.{xx≤-7或x>1},14.
![]() ,15.m=±2,16.-3< m<0
,15.m=±2,16.-3< m<0
三、解答题:
17、解析:⑴ ∵当x+2≥0时,x+2=x+2,x+2>x+2无解.
当x+2<0时,x+2=-(x+2)>0>x+2
∴当x<-2时,|x+2|>x+2
∴不等式的解集为{x|x<-2}
⑵原不等式等价于不等式组
|
由①得x≤-1或x≥5;
由②得-7<x<11,把①、②的解表示在数轴上(如图),
∴原不等式的解集为{x-7<x≤-1或5≤x<11}.
18、解析:(1)原不等式可化为:![]() 若a>1时,解为1<x<a,若a>1时,
若a>1时,解为1<x<a,若a>1时,
解为a<x<1,若a=1时,解为![]()
(2)△=![]() .
.
①当![]() ,△>0.
,△>0.
方程![]() 有二实数根:
有二实数根:![]()
∴原不等式的解集为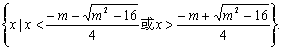
①当![]() =±4 时,△=0,两根为
=±4 时,△=0,两根为![]()
若![]() 则其根为-1,∴原不等式的解集为
则其根为-1,∴原不等式的解集为![]() .
.
若![]() 则其根为1,∴原不等式的解集为
则其根为1,∴原不等式的解集为![]() .
.
②当-4<![]() 时,方程无实数根.∴原不等式的解集为R.
时,方程无实数根.∴原不等式的解集为R.
19.解析:![]() ,比较
,比较![]()
因为![]()
(1)当k>1时,3k-1>k+1,A={xx≥3k-1或x![]() }.
}.
(2)当k=1时,x![]() .
.
(3)当k<1时,3k-1<k+1,A=![]() .
.
B中的不等式不能分解因式,故考虑判断式![]() ,
,
(1)当k=0时,![]() .
.
(2)当k>0时,△<0,x![]() .
.
(3)当k<0时,![]() .
.
故:当![]() 时,由B=R,显然有A
时,由B=R,显然有A![]() ,
,
当k<0时,为使A![]() ,需要
,需要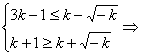 k
k![]() ,于是k
,于是k![]() 时,
时,![]() .
.
综上所述,k的取值范围是:![]()
20.解析: (1)当m2-2m-3=0,即m=3或m=-1时,
①若m=3,原不等式解集为R
②若m=-1,原不等式化为4x-1<0
∴原不等式解集为{x|x<![]() =,不合题设条件.
=,不合题设条件.
(2)若m2-2m-3≠0,依题意有
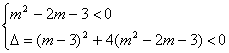 即
即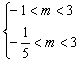
∴-![]() <m<3
<m<3
综上,当-![]() <m≤3时,不等式(m2-2m-3)x2-(m-3)x-1<0的解集为R.
<m≤3时,不等式(m2-2m-3)x2-(m-3)x-1<0的解集为R.
21.解析: 由已知得x1=-![]() ,x2=
,x2=![]() 是方程x2+px+q=0的根,
是方程x2+px+q=0的根,
∴-p=-![]() +
+![]() q=-
q=-![]() ×
×![]()
∴p=![]() ,q=-
,q=-![]() ,∴不等式qx2+px+1>0
,∴不等式qx2+px+1>0
即-![]() x2+
x2+![]() x+1>0
x+1>0
∴x2-x-6<0,∴-2<x<3.
即不等式qx2+px+1>0的解集为{x|-2<x<3}.
22.解析:由不等式![]() 的解集为
的解集为![]() ,得
,得
2和4是方程![]() 的两个实数根,且
的两个实数根,且![]() .(如图)
.(如图)
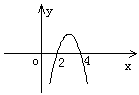
![]()
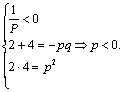
解得![]()
注:也可从![]() 展开,比较系数可得.
展开,比较系数可得.