高一数学同步测试（3）—简易逻辑
一、选择题：
1．若命题p：2n－1是奇数，q：2n＋1是偶数，则下列说法中正确的是 （ ）
A．p或q为真 B．p且q为真 C． 非p为真 D． 非p为假
2．“至多三个”的否定为 （ ）
A．至少有三个 B．至少有四个 C． 有三个 D． 有四个
3．“△ABC中，若∠C=90°，则∠A、∠B都是锐角”的否命题为 （ ）
A．△ABC中，若∠C≠90°，则∠A、∠B都不是锐角
B．△ABC中，若∠C≠90°，则∠A、∠B不都是锐角
C．△ABC中，若∠C≠90°，则∠A、∠B都不一定是锐角
D．以上都不对
4．给出4个命题：
①若
，则x=1或x=2；
②若
，则
；
③若x=y=0，则
；
④若
，x＋y是奇数，则x，y中一个是奇数，一个是偶数．
那么： （ ）
A．①的逆命题为真 B．②的否命题为真
C．③的逆否命题为假 D．④的逆命题为假
5．对命题p：A∩
＝，命题q：A∪＝A，下列说法正确的是 （ ）
A．p且q为假 B．p或q为假
C．非p为真 D．非p为假
6．命题“若△ABC不是等腰三角形，则它的任何两个内角不相等.”的逆否命题 是 （ ）
A．“若△ABC是等腰三角形，则它的任何两个内角相等.”
B．“若△ABC任何两个内角不相等，则它不是等腰三角形.”
C．“若△ABC有两个内角相等，则它是等腰三角形.”
D．“若△ABC任何两个角相等，则它是等腰三角形.”
7．设集合M={x x＞2}，P={xx＜3}，那么“x∈M，或x∈P”是“x∈M∩P”的 （ ）
A．必要不充分条件 B．充分不必要条件
C．充要条件 D．既不充分也不必要条件
8．有下列四个命题：
①“若x＋y=0 ，则x ，y互为相反数”的逆命题；
②“全等三角形的面积相等”的否命题；
③“若q≤1，则x2＋2x＋q=0有实根”的逆否命题；
④“不等边三角形的三个内角相等”逆命题；
其中的真命题为 （ ）
A．①② B．②③ C．①③ D．③④
9．设集合A={xx2＋x－6=0}，B={xmx＋1=0} ，则B是A的真子集的一个充分不必要的条件是 （ ）
A．
B．m=
C．
D．
10．“
”的含义是
（ ）
A．
不全为0 B． 全不为0
C．至少有一个为0
D．
不为0且
为0，或不为0且为0
11．如果命题“非p”与命题“p或q”都是真命题，那么 （ ）
A．命题p与命题q的真值相同 B．命题q一定是真命题
C．命题q不一定是真命题 D．命题p不一定是真命题
12．命题p：若A∩B=B，则
；命题q：若
，则A∩B≠B．那么命题p与命题q的关系是
（ ）
A．互逆 B．互否 C．互为逆否命题 D．不能确定
二、填空题：
13．命题“若△ABC是等腰三角形，则它的任何两个内角不相等”的逆否命题是
14．由命题p:6是12的约数，q:6是24的约数，构成的“p或q”形式的命题是：_ ___，“p且q”形式的命题是__ _，“非p”形式的命题是__ _.
15．设集合A={xx2＋x－6=0}， B={xmx＋1=0}，则B是A的真子集的一个充分不必要的条件是__ __.
16．设集合M={xx＞2}，P={xx＜3}，那么“x∈M，或x∈P”是“x∈M∩P”的
三、解答题：
17．命题：已知a、b为实数，若x2＋ax＋b≤0 有非空解集，则a2－ 4b≥0.写出该命题的逆命题、否命题、逆否命题，并判断这些命题的真假．
18．已知关于x的一元二次方程 (m∈Z)
① mx2－4x＋4＝0 ② x2－4mx＋4m2－4m－5＝0
求方程①和②都有整数解的充要条件.
19．分别指出由下列各组命题构成的逻辑关联词“或”、“且”、“非”的真假．
（1）p: 梯形有一组对边平行；q：梯形有一组对边相等．
（2）p: 1是方程
的解；q：3是方程的解．
（3）p: 不等式
解集为R；q: 不等式
解集为
．
（4）p: 
20．已知命题
；
若
是
的充分非必要条件，试求实数
的取值范围．
21．已知命题p:x2－x｜≥6，q：x∈Z，且“p且q”与“非q”同时为假命题，求x的值.
22．已知p:方程x2＋mx＋1=0有两个不等的负根；q:方程4x2＋4(m－2)x＋1＝0无实根．若“p或q”为真，“p且q”为假，求m的取值范围．
参考答案
一、选择题： ABBAD CACBA BC
二、填空题：
13.若△ABC有两个内角相等，则它是等腰三角形．
14.6是12或24的约数；6是12的约数，也是24的约数；6不是12的约数．
15.m=(也可为
)． 16.必要不充分条件．
三、解答题：
17．解析：逆命题：已知a、b为实数，若
有非空解集.
否命题：已知a、b为实数，若
没有非空解集，则
逆否命题：已知a、b为实数，若则没有非空解集．
原命题、逆命题、否命题、逆否命题均为真命题.
18.解析：方程①有实根的充要条件是
解得m
1.
方程②有实根的充要条件是
，解得
故m=－1或m=0或m=1.
当m=－1时，①方程无整数解.当m=0时，②无整数解；
当m=1时，①②都有整数.从而①②都有整数解m=1.反之，m=1①②都有整数解.
∴①②都有整数解的充要条件是m=1.
19．解析：⑴∵ p真，q假， 
“p或q”为真，“p且q”为假，“非p”为假．
⑵∵ p真，q真， “p或q”为真，“p且q”为真，“非p”为假．
⑶∵ p假，q假， “p或q”为假，“p且q”为假，“非p”为真．
⑷∵ p真，q假， “p或q”为真，“p且q”为假，“非p”为假．
20．解析：由
，得
． ：
．
由
，得
．
：B={
}．
∵是的充分非必要条件，且
， A
B．
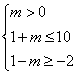即
21、解析： ∵p且q为假
∴p、q至少有一命题为假，又“非q”为假
∴q为真，从而可知p为假.
由p为假且q为真，可得：
即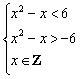
∴
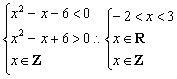
故x的取值为：－1、0、1、2.
22.解析： 若方程x2＋mx＋1=0有两不等的负根，则
解得m＞2，
即p：m＞2
若方程4x2＋4(m－2)x＋1＝0无实根，
则Δ＝16(m－2)2－16＝16(m2－4m＋3)＜0
解得：1＜m＜3.即q：1＜m＜3.
因“p或q”为真，所以p、q至少有一为真，又“p且q”为假，所以p、q至少有一为假，
因此，p、q两命题应一真一假，即p为真，q为假或p为假，q为真.
∴
解得：m≥3或1＜m≤2.