高一数学第二学期期中考试试卷
高一 得分
本试卷满分150分 考试时间120分钟 命题 毛大江 校对 丁俊影
选择题：本大题共12小题，每小题5分，共60分．在每小题给出
的四个选项中，只有一项是符合题目要求的．
1．cos
的值等于 A、
B、
C、－
D、－
（ ）
2. 若α是第二象限角，则π－α是 （ ）
A、 第一象限角 B、第二象限角 C、第三象限角 D、第四象限角
3. 已知
，则tan
的值是
（ ）
A、±
B、 C、- D、无法确定
4. 在半径为2的圆中，圆心角为
所对的弧长是
（ ）
A、
π
B、
C、
D、
π
5. 函数
的值域是
（ ）
A、[-2，2] B、{-2，2} C、{-2，0，2} D、{0，1，2}
6. 对于α∈R，下列等式中恒成立的是 （ ）
A、cos(-α)=-cosα B、sin(2π-α)=sinα
C、cos(π-α)=cos(π+α) D、tan(π+α)=tan(2π-α)
7. 函数
的图象的一条对称轴的方程是（
）
A、
B、
C、
D、
8.已知角
的 终边上有点P（7，－24），则cos的值为 （ ）
A、－
B、－
C、
D、
9.下列不等式中，正确的是 （ ）
A、
B、ecos52°<ecos53°
C、πtan109°>πtan110°
D、(
)sin115°<()sin116°
10. 若α，β为锐角，sinα=
,sin(α+β)=
, 则 cosβ= ( )
A、
B、
C、
或
D、-
11.若等腰三角形的底角余弦为
，则顶角的正弦值是
（ ）
A、±
B、
C、-
D、±
12.方程sinx=lgx的实根个数为
A、4个 B、3个 C、2个 D、1个 （ ）
一、 填空题：本大题共4小题，每小题5分，共20分．把答案填在题中横线上．
13.不查表不用计数器计算sin
的值为
14.arccos
－arctan1=
15.函数y=sin2x-2cosx的值域为
16.若函数y=3cos(ωx+
)的周期为T，且T∈(2，3)，则正整数ω是________。
三、解答题：本大题共6小题，共70分．
17. （本小题满分10分）已知sinx+cosx=m，
（1）求实数m的取值范围；
（2）当m取最大值时，求x的值
18. （本小题满分12分）化简sin130°（1+
tan190°）
19. （本小题满分12分） 已知：sin(
－x)=
，x
(0, )，
求cos2x的值
20. （本小题满分12分）设f(n)=sin(
+α)，
求f(1)·f(5)＋f(3)·f(7)的值
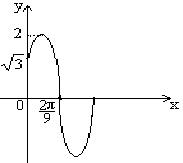
21. （本小题满分12分）函数y=Asin(ωx+φ)（A>0，ω>0，0<φ<2π）的一段图象如图，
（1）求A的值 （2）求φ的值 （3）求ω的值
22.（本小题满分12分）已知方程x2＋4ax＋3a＋1=0(a为大于1的常数)的两根为tanα，tanβ，且α，β均在区间（－
，）内，求tan
的值。
高一第二学期期中考试
高一数学答案
一．选择题：1.D 2.A 3.B 4.A 5.C 6.C 7.D 8.B 9.D 10.B 11.B 12.B
二．填空题：13.
14.
15.
16. 3
三．解答题：
17．解⑴
m=sinx+cosx=
sin
m的范围是[-,]……………….4分
⑵由⑴得x+
=2k
+
,即当x=2k+
时m取得最大值……..…7分
x+=2k- 即当x=2k-
时m取得最小值-……….10分
18．解sin130º(1+tan190º)=sin50 º(1+tan10º)……………………………2分
= sin50 º
……………………4分
= sin50 º
…………………………8分
=
…………………………………10分
=
=1…………………………………………12分
19．解x(0,),sin(-x)=
cos(-x)= 
………………..……………3分
cos2x=sin(-2x)=sin2(-x)………………………………………6分
=2sin(-x)cos(-x)………………………………………9分
=2××=
……………………………………………12分
20．解f(1)f(5)+f(3)f(7)=sin(+α)sin(
+α)+sin(+α)sin(
+α)……………4分
=－sin2(+α) －sin2(+α)………………………………8分
=－[sin2(+α)+cos2(+α)]=－1…………………………..12分
21．解 ⑴ A>0
由图得A=2…………………………………………………………2分
⑵
图象过点(0,) =2sinφ
sinφ=
…………………………………………………………………4分
0<φ<2 φ=
或
………………………………….…………6分
又 (0,)为单调递增上的点
φ=…………………………………………………………………8分
⑶
由 ⑴ ⑵ 知 y=2sin(
x+)
0=2sin(
+)………………………………………………10分
又点（，0）在单调递减区间上
+= =3………………………………………………12分
22．解由
=(4a)2－4(3a+1)>0得a>1或a<－
(舍去)……………………………2分
tanα、tanβ是方程的两根
tanα+tanβ=－4a<0, tanαtanβ=3a+1>0…………………………4分
又α、β∈(－,)
α、β∈(－,0), α+β∈(－,0)……………………………6分
tan(α+β)=
=
=
…………………8分
=
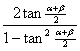…………………………………………………10分
tan
=-2或tan=
(舍去)…………………………12分