一、选择题 （每题5分，共60分）
1．已知集合
，则集合A中的元素有----------------------（ ）
（A）3个 （B）4个 （C）5个 （D）6个
2．设M和m分别表示函数
的最大值和最小值，则M+m等于-----------（ ）
（A）1 （B）2 （C）－2 （D）－1
3．已知
，则
的值为----------------------------------------------（ ）
（A）
（B）
（C）
（D）
4．已知角
的终边经过点
，则=---------------------------------（ ）
（A）
（B）
（C）
（D）
5．函数
＝sin2ωx－cos2ωx (ω＞0)的最小正周期为1，则----------------------------（ ）
（A）ω＝1，是偶函数 （B）ω＝π，是偶函数
（C）ω＝1，是奇函数 （D）ω＝π，是奇函数
6．在
内，使
成立的
的取值范围为-----------------------------------（ ）
（A）
（B）
（C）
（D）
7．已知
，则
的值是-------------------------------------------------（ ）
（A）2 （B）－2
（C） （D）
8．已知
的图象----------------------（ ）
（A）与g(x)的图象相同 （B）与g(x) 图象关于y轴对称
（C）是由g(x)的图象向左平移
个单位得到的
（D）是由g(x)的图象向右平移个单位得到的
9．已知A、B、C是△ABC的三个内角，且
，则------------------（ ）
(A) B=C (B) B＞C (C) B＜C (D) B,C的大小与A的值有关
10．
中，
，则角C等于 （
）
（A）
（B）
（C）
（D）120
11．若A,B,C是△ABC的三个内角，且
，则下列结论中正确的是（ ）
（A）
（B）
（C）
（D）
12．如果函数满足：对于区间D内的任意
，有
成立，那么称为凸函数。已知函数
在区间
上是凸函数，则在△ABC中，sinA+sinB+sinC的最大值是----------------------------------------------------------------------------------------------（ ）
（A）
（B）
（C）
（D）
二、填空题 （每题4分，共16分）
13．计算1-2
=_____________________（不取近似值）
14．如果
，那么的值是___________________
15．函数
的值域是 ________________________
16．设函数
，若
是偶函数，则
的一个可能值是_________________
三、解答题
17．（10分）求证：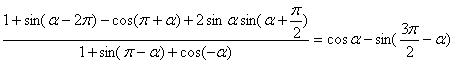
高 一 数 学 第 二 张 试 卷
18．（12分）已知
求
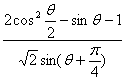的值。
19．（12分）用“五点法”画出函数
的图像，并指出这个函数的周期与单调区间，以及此图像是由的图像经过怎样的变换得到的。
高 一 数 学 第 三 张 试 卷
20．（14分）已知
若f(x)的最大值为3，求实数m的值。
21．（14分）已知
（Ⅰ）若
分别求
的值；
（Ⅱ）试利用正弦函数的单调性比较
的大小.
高 一 数 学 第 四 张 试 卷
22．（14分）某港口的水深
（米）是时间（
，单位：小时）函数，下面是该港口的
水深表：
|
| 0 | … | 3 | … | 9 | … | 15 | … |
|
| 10 | … | 13 | … | 7 | … | 13 | … |
|
|
经过长时间的观察，描出的曲线如图所示，
 |
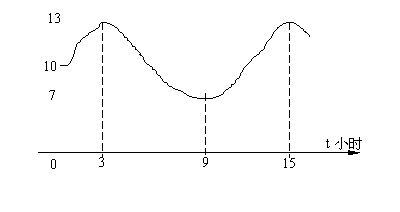经过拟合，该曲线可近似地看成正弦函数
（其中A.>0,ω>0）的图象。
（1）试根据数据表和曲线，求函数
（其中A.>0,ω>0）的表达式；
（2）一般情况下，船舶航行时船底同海底的距离不小于4.5米时是安全的，如果某船的吃水深度（船底与水面的距离）为7米，那么该船在什么时间段能够安全进港？若该船欲当天安全离港，它在港内停留的时间最多不能超过多长时间？（忽略离港所用的时间）