高一数学第一次月考试卷
一、 选择题：（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的.请把选出的答案涂在答题卡上）
1、
之间与
终边相同的角是
（ ）
（A）
（B）
（B）
（D）
2、已知sin(π－α)＝
，那么cos(
－α)的值为
( )
（A）－ （B）
（B）－
（B）
3、sin11
sin18
－cossin2＝
（ ）.
（A）
（B）－ （C）
（D）－
4、若
，则
等于
（ ）
（A）1 （B）－1 （C） 2 （ D）－2
5、若θ是第四象限角，且满足sin
=－sin，则在
（ ）.
（A）第一象限 （B）第二象限 （C）第三象限 （D）第四象限
6、设a<0,角α的终边经过点P(-3a,4a),那么sinα+2cosα的值等于( )
（A）
（B） -
（C） 
（D -
7、设
角的终边上一点P的坐标是
，则等于 （ ）
（A）
（B）
（C）
（D） 
8、
=
（ ）
（A）
（B）1 （C）
（D）2
9、sin5
·(1+tan1)的值是
（ ）.
（A）
（B）1 （C） （D）2
10、已知tgα=2，则
的值等于
（ ）.
（A）
（B）
（C）
（D）
11、已知sin＝
，cos＝
,则θ的终边在 （ ）
（A）第一象限 （B）第二象限 （C）第三象限 （D）第四象限
12、设0<α<π，sinα+cosα=
, 则cos2α的值是 （ ）.
（A）±
（B） ±
（C）－ （D）
高一数学第一次月考答卷 座位号_____
二、填空题（每题4分，共16分）
13、计算：
14、用弧度制表示终边在x轴上的角的集合为
15、已知扇形的圆心角是1弧度,扇形的周长是6
，则扇形的面积是_
16、已知sin(4
－α)=－
，4<α<90°, 那么sinα=
三、解答题（共74分）
17、（本题满分12分）已知cosα=－,求sinα, tanα的值.
18、（本题满分12分）△ABC中，cosA＝－
, sinB＝
, 求cosC.
19、（本题满分14分，第一小题6分，第二小题8分）
（1）化简：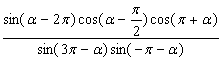
(2)求证：tanα=
20、（本题满分12分）已知三角形ABC的三个内角为A、B、C，若tanA tanB>1,
求证：三角形ABC是锐角三角形（注：三内角都是锐角的三角形叫锐角三角形）.
21、（本题满分12分）已知一元二次方程
的两根为tanα, tanβ , 求,cos(α+β)的值.
22、（本题满分12分）如图，扇形AOB的半径为，扇形的圆心角为
，PQRS是扇形的内接矩形，设∠AOP=θ，
（1） 试用θ表示矩形PQRS的面积y；
（2）利用正、余弦的和（差）与倍角公式化简矩形面积表达式y.
高一数学第一次月考答案
一选择题1—6 ABBCDA 7—12 DCBADC
二、填空题（每题4分，共16分）
13、计算：
14、用弧度制表示终边在x轴上的角的集合为{αα=Kπ,k∈Z}
15、已知扇形的圆心角是1弧度,扇形的周长是6，则扇形的面积是2 cm2
16、已知sin(4－α)=－，4<α<90°, 那么sinα=
三、解答题（共74分）
17、（本题满分12分）已知cosα=－,求sinα, tanα的值.
解：因cosα=－﹤0，且≠±1，所以α的终边在二或三象限；
ⅰ、
α在二象限时，sinα=
ⅱ、α在三象限时sinα=
18、（本题满分12分）△ABC中，cosA＝－, sinB＝, 求cosC.
解：因cosα=－﹤0, 所以 900
﹤A﹤1800(A为三角形内角)，
从而00﹤B﹤900
所以sinA=
cosB=
cos(A+B)=cosAcosB－sinAsinB=－
因为A+B=1800－C
所以cosC= －cos(A+B)=
19、（本题满分14分，第一小题6分，第二小题8分）
（1）化简：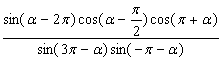
解：原式=－cosα
(2)求证：tanα=
证明：略
20、（本题满分12分）已知三角形ABC的三个内角为A、B、C，若tanA tanB>1,
求证：三角形ABC是锐角三角形（注：三内角都是锐角的三角形叫锐角三角形）.
证明：因tanA tanB>1>0，所以tanA与tanB同号，若都为负值，因A、B都在00到1800之间，所以都为钝角，与三角形内角和为1800矛盾，所以tanA与tanB都为正，从而A、B都是锐角；
由tanA tanB=
>1
A、B都是锐角，所以cosA、 cosB都为正
可化为sinAsinB>cosAcosB
即cos(A+B)<0 因为A+B=1800－C
所以cosC>0 因为00﹤A﹤1800
所以C是锐角,
从而A、B、C都是锐角
即三角形ABC是锐角三角形
21、（本题满分12分）已知一元二次方程的两根为
tanα, tanβ , 求,cos(α+β)的值.
解：因tanα+ tanβ=－
，tanαtanβ=3
所以tan(α+β)= 
>0
即α+β的终边在一或三象限；
ⅰ、 α在一象限时，cos(α+β)= 
ⅱ、α在三象限时cos(α+β)= －
22、（本题满分12分）如图，扇形AOB的半径为，扇形的圆心角为，PQRS是扇形的内接矩形，设∠AOP=θ，
（1） 试用θ表示矩形PQRS的面积y；
（2）利用正、余弦的和（差）与倍角公式化简矩形面积表达式y.
解：（1）在直角三角形OPS中
SP=sinθ，OS=cosθ
矩形的宽SP=sinθ
因∠ROQ=
所以OR=RQ=SP=sinθ
矩形的长RS=OS－OR=cosθ－sinθ
所以面积：y=(cosθ－sinθ)sinθ (0﹤θ<)
(2) y=2 sinθcosθ－2sin2θ=sin2θ－(1－cos2θ)
= sin2θ+cos2θ－1=sin(2θ+)－1
(或cos(2θ－)－1) (0﹤θ<)