高一数学第一学期期末调研试试题A
本试卷分第I卷（选择题）和第II卷（非选择题）两部分，第I卷1至2页（第1至10题），第II卷3至8页（第11至20题）共150分，考试时间120分钟。
第I卷（选择题共50分）
注意事项：
1、答第I卷前，考生务必将本人的学校、班级、姓名、考试号填在第II卷的密封线内。
2、将第I卷上每小题所选答案前的字母标号填写在第II卷卷首相应的答题栏内，在第I卷上答题无效。
3、考试结束，只交第II卷。
一、选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个选项项中，只有一项是符合题目要求的。
1．如果S={1，2，3，4，5}，M={1，3，4}，N={2，4，5}，那么（CSM）
（CSN）等于
（A）
（B）{1，3}
（C）{4}
（D）{2，5}
2．函数y=lg(2x-x2)的定义域是
（A）（0，2） （B）[0，2]
（C）
（D）
3．a、b、c成等比数列，那么关于x的方程ax2+bx+c=0
（A）一定有两不等实根 （B）一定有两相等实根
（C）一定无实根 （D）一定有两符号不相同的实根
4． 函数y=2x+a的图象不经过第二象限，则
（A）a<0
（B）a
（C）a<-2
（D）a<-1
5． 已知等比数列{an}的前三项分别为a，a+1，a+3(a
)，则它的公比q等于
（A）1 （B）2 （C）3 （D）不能确定
6． 在等比数列中，a1=1，公比q，且q
，若
，那么m等于
（A）44 （B）45 （C）46 （D）47
7．x<2是x+1<1的
（A）充分非必要条件 （B）必要非充分条件
（C）充要条件 （D）既非充分也非必要条件
8．函数f(x)=lgx则对任意正实数x、y都有
（A）f(xy)=f(x)f(y) （B）f(xy)=fx)+f(y)
（C）f(x+y)=f(x)f(y) （D）f(x+y)=f(x)+f(y)
9．等差数列{an}的前n项和用Sn表示，已知a1<0，公差d>0，S6=S11，下述结论中正确的是
（A）S10最小 （B）S9最大 （C）S8，S9最小 （D）S8，S9最大
10．直线y=1与函数y=logax的图象交于A、B两点，则AB等于
（A）1 （B）2 （C）a （D）2a
第II卷（非选择题共100分）
注意事项：
用钢笔或圆珠笔直接写在试题卷上。
二、填空题：本大题共4分小题，每小题5分，共20分。把答案填在题中的横线上。
11、函数f(x)=log2(x-1) (x>1)的反函数是___________.
12、设f(x)是定义在R上的奇函数，若当x>0时，f(x)=log3(1+x)，则f(-2)=_______。
13、已知
，数列{an}满足
，且a1=1，则a5=_____.
14、函数f( x)=ax(a>0，且a)，在[1，2]中的最大值比最小值大
，则a的值为______.
三、解答题：本大题共6小题，共80分。解答应写出文字说明、证明过程或演算步骤。
15．（本小题满 分13分）
等差数列{an}中，前n项和用Sn表示。已知S5=35，S10=120。求：（1）Sn ；（2）an
16．（本小题满 分13分）
设函数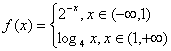
，求满足
的x的值。
17．（本小题满 分13分）
设集合A={x x-a<2}，B={xx2-x-6<0}
(1)当a=2时，求
；(2)若
，求实数a的取值范围。
18．（本小题满 分13分）
光线通过一块玻璃，其强度要损失10%，把几块这样的玻璃重叠起来。设光线原来的强度为
，通过x块玻璃以后强度为y。
（1）写出y关于x的函数关系式。
（2）通过多少块玻璃以后，光线强度减弱到原来的
以下。（lg3
）
19．（本小题满 分13分）
已知f(x)=
的图象过点A（4，
）和B（5，1）
（1）求f(x)的解析式；（2）记an=log2f(n)，n
。数列{an}前n项和用Sn表示，解关于n的不等式
.
20．（本小题满 分13分）
定义在
上的奇函数f(x)，已知f(-2)=0,f(x)在x>0时递减。
（1）求f(x)<0的解集；
（2）如果a+b<0，ab<0，判断f(a)+f(b)的正负，并说明理由。
高一数学A答案
一、选择题：（第小题5分，共50分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A | A | C | B | B | C | B | B | C | D |
二、填空题：（每小题5分，共20分）
11．
12.-1
13. 
14.
三、解答题：
15．解法一：设等差数列{an}的公差为d，则
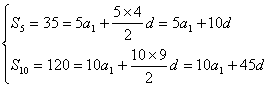
解得 a1=3，d=2
所以
解法二：设
，则
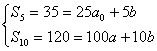解得a=1，b=2
16．（本小题满分13分）
当x
时，由
，得x=2，但
，舍去。
当x
时，由
，得x=
，但
。
综上所述，x=
17．（本小题满分13分）
（1）因为A={x0<x<4}，B={x-2<x<3} 所以
（2）因为A={xa-2<x<a+2}，B={x-2<x<3}
因为
所以
解得，
18．（本小题满分13分）
（1）
光线经过1块玻璃后强度为（1-10%）=0.9
光线经过2块玻璃后强度为（1-10%）
光线经过3块玻璃后强度为（1-10%）
……
光线经过x块玻璃后强 度为
所以y=
（2）由题意：
，所以
两边取对数，xlg0.9<
因为lg0.9<0，所以
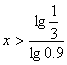
因为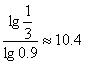
所以xmin=11
答：通过11块玻璃以后，光线强度减弱到原来的以下。
19．（本小题满分13分）
（1）因为f(x)=的图象过点A(4,)和B（5，1）
所以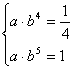
解得，b=4,a=
所以
(2)an=log2f(n)=2n-10
所以，即2n(n-5)(n-9)
因为n>0，所以
又因为
所以
20．（本小题满分13分）
（1）因为f(x)是定义在上的奇函数，且f(-2)=0，所以f(2)= -f(-2)=0
当x>0时，f(x)<0，即f(x)<f(2)
又因为f(x)在x>0时递减，所以x>2
当x<0 时，-x>0，f(x)<0即f(-x)>0，即f(-x)>f(2)
所以-x<2，即x>-2，又因为x<0，所以-2<x<0
综上所述，f(x)<0的解集为
（2）当a<0，b>0时，因为a+b<0,ab<0，所以-a>b>0
因为f(x)在x>0时递减，所以f(-a)<f(b)
因为f(x)是定义在上的奇函数，所以f(-a)= -f(a)
所以-f(a)<f(b)，所以f(a)+f(b)>0
同理，当a>0，b<0时，也有f(a)+f(b)>0
综上所述，f(a)+f(b)>0