高一数学第一学期期末统一考试
一、选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有一项是合题目要求的，将正确答案的选项字母填在括号内。
1．设全集U={1，2，3，4，5，6，7}，集合A={1，3，5}，集合B={2，3，6}，则
=（ ）
A．{1，5} B．{3} C．{1，3，4，5，7} D．{4，7}
2．如果一个命题的逆命题是真命题，则它的否命题（ ）
A．一定是假命题 B．不一定是假命题 C．一定是真命题 D．不一定是真命题
3．已知命题p：“-2<x<0”，命题q：“x<2”，则p是q的（ ）
A．充分不必要条件 B．必要不充分条件 C．充分必要条件 D．既不充分又不必要条件
4．函数
的反函数是（ ）
A．
B．
C．
D．
5．下列函数中，既是其定义域上的是单调函数，又是奇函数的是（ ）
A．
B．
C．
D．
6．在等差数列
中，
，则
（ ）
A．-22 B．-24 C．60 D．64
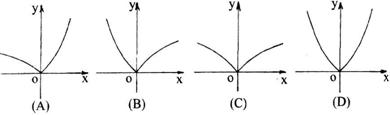
7．函数
的图象大致是（ ）
8．在等比数列中，
，则
（ ）
A．210 B．360 C．480 D．720
9．设二次函数f(x)的图象关于直线x=1对称，并且当x>1时f(x)是增函数，又设a=f(1-π)，
b=f(π-1)，
，则实数a、b、c的关系是（ ）
A．a=b>c B．a>b>c C．c>b>a D．c>a=b
10．已知函数
，（其中a、b为常数，且a>1，b>0），若x∈（1，+∞）时，f(x)>0恒成立，则（ ）
A．a-b≥1 B．a-b>1 C．a-b≤1 D．a=b+1
二、填空题：本大题共4小题，每小题4分，共16分。把答案填在题中横线上。
11．若
，则
。
12．已知函数f(x)满足
，则f(x)的解析式为f(x)=__________________。
13．函数
在[-1，1]上的最大值和最小值分别是__________________。
14．若等差数列中，
，
表示数列的前n项和，且
，则取最大值时n=__________________。
三、解答题：本大题共5小题，共34分。解答应写出文字说明、证明过程或演算步骤。
15．（本小题满分6分）
已知奇函数f(x)的定义域是{xx∈R，且x≠0}，当x<0时，f(x)=xlg(2-x)，求x>0时，f(x)的解析式。
16．（本小题满分6分）
已知三个数a、b、c成等比数列，其积为8，又a、b、c-1成等差数列，求这三个数组成的数列。
17．（本小题满分7分）
已知某地区现有人口50万。
（I）若人口的年自然增长率为1.2%，试写出人口数y（万人）与年份x（年）的函数关系；（II）若20年后该地区人口总数控制在60万人，则人口的年自然增长率应为多少？ （
）
18．（本小题满分7分）
已知等比数列的各项都是正数，
，且在前n项中，最大项的值为54，求n的值。
19．A（重点校学生做，普通校学生选做，本小题满8分）
已知二次函数
满足f(1)=0。
（I）若a>b>c，证明f(x)的图象与x轴有两个交点，且这两个交点间的距离d满足：
；
（II）设f(x)在
处取得最小值，且对任意实数x，等式
（其中n∈N，
）都成立，若数列
的前n项和为
，求的通项公式。
19．B（普通校学生做，重点校学生不做。本小题满分8分）
已知a、b为常数，且a≠0，函数
，且f(3)=1，又方程f(x)=x有唯一解。
（I）求f(x)的解析式及方程f(x)=x的解；
（II）当
，数列
是何数列？请说明理由。
2003～2004高一（上）数学期末考试答案
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | C | C | A | D | B | B | A | C | B | A |
二、填空题
11．a-2 12．
13．2，
； 14．6
三、解答题
15．解：∵x<0时，f(x)=xlg(2-x)，又f(x)为奇函数，且当x>0时，-x<0 …………2分
∴f(x)=-f(-x) ……………………………………………………………………………4分
=-{(-x)lg[2-(-x)]}=xlg(2+x)。
即x>0时，f(x)=xlg(2+x)…………………………………………………………………6分
16．解：设
，c=bq，
。解得b=2。
即
，b=2，c=2q …………………………………………………………………2分
∵2b=a+(c-1)，
。
。∴q=2或。 …………4分
当q=2时，a=1，b=2，c=4；
当
时，a=4，b=2，c=1。
即所求数列为1、2、4或4、2、1。 ………………………………………………6分
17．解：（I）x年后
。 …………………………………………3分
（II）设年人口自然增长率为p，因此有
……………………5分
即
。时 解得
。于是p=0.009。
即人口年自然增长率为0.9%。……………………………………………………7分
18．解：由已知
，得q>0。若q=1，则
。
但
。∴q≠1 ………………………………………………1分
，①÷②得
。……2分
∴q>1。又
，
是递增数列。
∴在前n项中，最大项为
。即
…………………………………………4分
。
。即
……………………5分
将代入①，得
。
。解得q=3。…6分
又
，∴n=4。 …………………………………………………………………7分
19．（重点校）（I）证明：∵f(1)=0，∴a+b+c=0。∴a>b>c，
∴a>0，c>0。∴ac<0。
…………………………………………………1分
即f(x)的图象与x轴有两个交点。∵f(1)=0，∴1是f(x)=0的一个根。
由根与系数的关系可知f(x)=0的另一个根是
。
。非曲直……………2分
。∵a>b>c，且b=-a-c，∴a>b=-a-c>c。
。
。
。即。………………3分
（II）解：∵f(x)在
处取得最小值，
是f(x)的对称轴方程。
由f(x)图象的对称性及f(1)=0可知f(t)=0。 ………………………………………5分
令x=1，得
；令x=t，得
由①，②解得
。…………………………………………………………7分
∴n>1时，
。又n=1时，
，
∴是首项为
，公比为q=t的等比数列，
。 …………………8分
（普通校）（I）
，……………1分
∵f(x)=x有唯一解，∴由
，解得b=1。 ……………………2分
又f(3)=1，∴3=3a+1。
。
。…………………………………3分
由
易解得方程f(x)=x的解为x=0。 ………………………………………4分
（II）由
（n>1），得
……6分
（n>1）。即当n>1时，是等差数列。 ………………………8分