高一第二学期数学期中考试试卷
(满分:100分 考试时间:120分钟)
一、选择题（共15小题，每小题3分，满分45分。将唯一正确的答案填在答题卷答题卡对应的题号下。）
1. 若
，则
角所在的象限是（ ）
（A）第一象限 （B）第二象限 （C）第三象限 （D）第四象限
2. 若角
的终边在射线
上，则
的值为（ ）
（A）
（B）
（C）
（D）
3. 下列命题中正确的是（ ）
（A）直平行六面体是长方体 （B）对角面是全等的矩形的四棱柱是长方体
（C）侧面都是矩形的直四棱柱是长方体 （D）底面是矩形的直四棱柱是长方体
4. 圆锥的侧面积为80，其侧面展开图的扇形圆心角为
，则圆锥底面面积为（ ）
（A）15 （B）60 （C）40 （D）30
5. 下列函数中同时满足①在区间
上是增函数；②以
为周期；③是偶函数三个条件的是（ ）
（A）
（B）
（C）
（D）
6. 
的图象的一条对称轴的方程是（ ）
（A）
（B）
（C）
（D）
7. 满足
的
的集合是（ ）
（A）
（B）
（C）
（D）
8. 在
中，若
，则的形状一定是（ ）
（A）钝角三角形 （B）等腰三角形 （C）直角三角形 （D）正三角形
9. 一个三棱锥中，两组相对棱所成的角都是
，则另一组相对棱所成的角为（ ）
（A）
（B）
（C）
（D）
10. 已知圆台上、下底面半径之和等于母线长的2倍，其侧面积为450，母线与底面所成的角为，
且
，那么圆台的高是（ ）
（A）12 （B）21 （C）6 （D）9
11. 函数
的单调递减区间是（ ）
（A）
（B）
（C）
（D）
12. 函数
的最小值为（ ）
（A）2 （B）0 （C）－1 （D）6
13. 若
（ ）
（A）
（B）
（C）
（D）
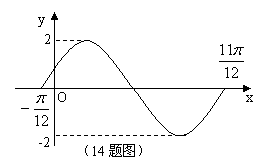14. 如图，已知函数
的图象（部分），则（ ）
（A）
（B）
（C）
（D）
15. 在半径为
的球面上有
两点，其球面距离为
，那么过
的球截面到球心的最大距离为（ ）
（A）
（B）
（C）
（D）
二、填空题(共5小题,每小题3分,满分15分)
16. 
.
17. 已知圆锥的底面面积为
，则它的中截面与底面间部分（圆台）的中截面的面积为 .
18. 已知
，若
.
19. 若正棱台的上、下底面面积及侧面面积之比为4∶9∶10，则其侧面与底面所成的角为 .
20. 长方体的共顶点的三个侧面面积为
则它的外接球的表面积为 .
三、解答题(共5题, 每题8分, 满分40分)
21．已知
求 
的值.
22．已知圆锥的高和底面半径均为. 请问：是否存在该圆锥的一个内接圆柱，使得圆柱的全面积是圆锥的全面积的
倍. 若存在，请求出圆柱的全面积；若不存在，请说明理由。
23．已知函数
的最大值为
，最小值为
. 求函数
的定义域、值域并指出它的单调递减区间.
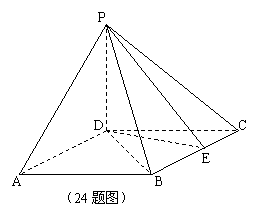
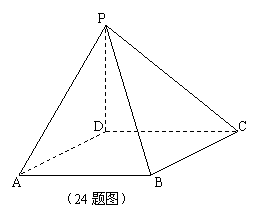24．（如图）已知四棱锥
的高为
,底面是边长为
的菱形，
侧面
和侧面
都垂直于底面，且二面角
为
.
试求：当为何值时，侧面
与底面所成的角为，
并求此时棱锥的全面积。
25．若函数
对任意实数
都有
恒成立，
求实数
的取值范围。
参考答案与评分标准
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 答案 | B | D | D | D | D | A | D | C | A | D | C | B | A | C | C |
二、填空题： 16；
17； 
18；－1 19；
20；
三、解答题(共5题, 每题8分, 满分40分)
21．解：由条件得： 
两边平方得： 
.
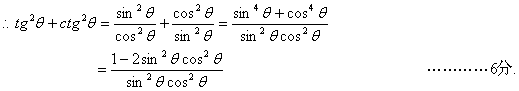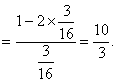
22．解：设存在满足题意的圆柱，且设它的底面半径为
，高为。则
由三角形相似可得
于是：
即 
故不存在满足题意的圆柱。
23．解：由题意得：
. 
值域为
；单调递减区间为
.
24．解：（如图）由侧面和侧面都垂直于底面知
因为底面是菱形，所以为正三角形，
取
，联接
，
则
为侧面与底面所成的角，
所以棱锥的全面积为
25．解：依题意必须且只需
由条件 
① 当
② 当
③ 当
综上讨论知：当