高一第一学期数学期终考试

高一第一学期数学期终考试

一、选择题（每小题3分，共计30分）（以下每个问题的四个选项中，有且只有一个选项是正确的）

1．已知数列3,3,3,3,3. 则该数列为（　　 ）

A．等差数列但不是等比数列　　　　　　　　 B．等比数列但不是等差数列

C．既是等差数列也是等比数列　　　　　　　 D．既不是等差数列也不是等比数列

2．设数列是递增的等差数列，前三项的和为15、积为80，则它的首项为（　 ）

A．1　　　　  B．2　　　　 C．4　　　　D．5

3．等比数列的前n项和为S_n=3ⁿ⁺¹－a，则实数a的值为（　 ）

A．3　　　　　　 B．　　　　  C．－3　　　　  D．－

4．在等比数列中，若前n项和S_n=25，前2n项和S_2n=100，则前3n项和S_3n=（　　）

A．325　　　　　 B． 225　　　　　  C． 200　　　　  D．175

5．设f(n)=1++……+，则必有(　　 )

A．f(1)=1　　　　B．f(1)=1+　　 C．f(1)=1+　　  D．f(1)=1+

6．已知函数f(x)=a^x(a>0且a)，则对于任意的实数x, y 都有(　　 )

A．f(xy)=f(x)f(y )　　 B．f(xy)=f(x)+f(y)　　C．f(x+y)=f(x)f(y )　  D．f(x+y)=f(x)+f(y)

7．某工厂去年12月份的产量是去年1月份产值的m倍，则该厂去年月产值的平均增长率为（　　）

A．　　　　B．　　  C．　　  D．

8．已知f(x⁵)=log₂x，则f(2)的值为（　　　）

A．1　　 　　B．5　　　　 C．－5　　 　　　D．

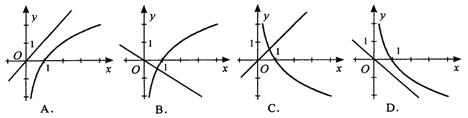9．当a>1时，函数y=log_ax和y=(1－a)x的图象只可能是（　　 ）

10．将函数f(x)的图象C向左平移2个单位得到C₁，再将C₁作关于y轴的对称图形得到C₂，有同学说，实际上只要作一个图形变换就可使C₂变换到C，那么，这变换是（　　）

A．关于直线x=1 对称　　　　B．关于直线x=－1对称

C．关于直线x=2对称　　　　 D．关于直线x=－2对称

二．填空题（每小题4分，共计24分）

11．已知两实数1与x的等差中项为4，若三个数1，y，x成等比数列，则y=______。

12．若一个等差数列的前3项和为34，最后3项的和为146，所有项的和为780，则这个数列的项数为_______________。

13．已知函数f(x)=2^－x，若f^－1(a)=4，则实数a=________________。

14．设函数f(x)=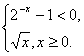若f(x₀)>1，则x₀的取值范围是_____________。

15．已知S_n表示等比数列的前n项和，a₁=1，，则该等比数列的公比q=_________.

16．使log₂(－x)<x+1成立的x的取值范围是____________。

三．解答题（本大题共计46分，附加题5分另计）

17．（本题8分）

求函数y=　 x的反函数。（注： y=e^x的反函数为 y=lnx, x

18．（本小题8分）

设为等差数列，已知a₃=11,a₈=31.

(1)　  求a_n；

(2)　  若S_n为数列的前n项和，T_n为数列的前n项和，求T_n。

19．（本小题10分）

在等差数列中，a₁=2，a₁+a₂+a₃=12。

(1) 求数列的通项公式；

(2) 令b_n=a_n·3ⁿ，求数列的前n项和S_n

20．（本小题10分）

有甲、乙两种商品，经销这两种商品所能获得的利润依次是p万元和q万元，它们与投入的资金x万元的关系有经验公式：p=x，q=。现有资金9万元投入销甲、乙两种商品，为了获取最大利润，问：对甲、乙两种商品的资金分别投入多少万元能获取最大利润？

21．（本小题10分）

已知c>0且c1,设P：函数y=(2c－1)·c^x在R上为减函数；

　　　 　　　　　　 Q：不等式x+(x－2c)²>1的解集为R

若P和Q有且仅有一个正确，求c的取值范围。

22．（附加题）（本小题满分5分，附加题分数可计入总分，但总分不超过100分）从1到10¹⁰这10¹⁰个自然数中，所有数位上有且只有一个零的自然数有多少个？（用最简表达式表示）

【参考答案】

一．选择题

1.C　　2.B　　3.A　　4.A　　 5.D　　6.C　　 7.D　　8.D　　9.B　　 10.A　　

二．填空题

11. 　　　　12.　26　　　13.　　　 14.(－1, 1)　　　 15.　 16.(－1,　0)

三．解答题

17.解：∵,　 ∴ 即　∴x=ln

∵x>0 ,　∴e^x>1.　  ∴y=1+.(法二：∴ y>1)

∴y=, x的反函数为y=ln.(x>1)

18.解：（1）设数列的公差为d，

则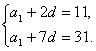　 ∴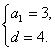　　∴a_n=4n－1

(2) 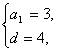 ∵　　 ∴S_n=2n²+n

∴　

∴

19.解：（1）设数列的公差为d

∵　　∴3　　  ∴　　

∴d=　　  ∴　

(2)∴　　　　 ∴……①

∴………②

①　　 －②得：

=

∴

20．解：设对乙商品投入x万元，则对甲商品投入9－x万元

设利润为y万元

∴y===

∴当=2,即x=4时，y_max=1.3

∴投入甲商品5万元，乙商品4万元时，能获得最大利润1.3万元.

21．解：当P为正确时，

∵函数y=（2c－1）·c^x 在R上为减函数，

∴　　或　　  ∴当P为正确时，.

当Q为正确时，

∵不等式x+(x－2c)²>1的解集为R，

∴当x时，x²－(4c－1)x+(4c²－1)>0恒成立.

∴△=(4c－1)²－4· (4c²－1)<0

∴－8c+5<0

∴当Q为正确时，c>.

由题设，若P和Q有且仅有一个正确，则

（1）P正确Q不正确

∴　　 ∴.　　

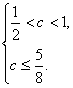（2）P不正确Q正确

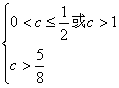　　  ∴c>1

∴综上所述，若P和Q有且仅有一个正确，c的取值范围是.

22．解：s=9+2×9²+3×9³+…+9×9⁹=9+9²+9³+…+9⁹+9(s－9¹⁰)=

∴s=