高一第一学期数学月考试卷
命题人：数学教研组
一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合要求的。
1、给出下列四个对应，其中构成映射的是：
|
|
|
|
|
|
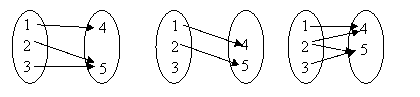
A、只有①、② B、只有①、④
C、只有①、③、④ D、只有③、④
二、已知全集U=
1， 2， 3， 4，5， 6，7，8
，A=3，4，5，B=1，3，6，7，则A
CUB等于：
A、2 ，4，5，8
B、3
C、4，5
D、Φ
3、已知U是全集，P、Q都是非空集合，P Q，则下列集合中空集是：
A、PQ B、（CUP）Q
C、PCUQ D、CUP CUQ
4、下列集合中，表示同一集合的是：
A、M=
（3，2）， N=（2，3）
B、M=3，2， N=2，3
C、M=（x，y）∣x+y=5，N=y∣x+y=5
D、M=2，3，N=（2，3）
5、下列图形中，不可能是函数的图像的是
6、下列函数中，在区间（0，1）上为增函数的是：
A、y=1－2x B、y=
C、y=x+1 D、y =2x2－x+3
7、如果奇函数f(x)在区间[3，7]上是增函数且最小值为5，那么f(x)在区间[－7，－3]上是：
A、增函数且最小值为－5 B、增函数且最大值为－5
C、减函数且最小值为－5 D、减函数且最大值为－5
8、已知函数f(x)=ax3+bx－2,且f(－2)=10,则f(2)等于：
A、－14 B、－12 C、－10 D、10、
9、若函数y=f(x)的图像经过点（0，－1），那么函数y=f(x+4)的图像经过点：
A、（4，－1） B、（－4，－1） C、（4，1） D、（－4，1）
10、已知函数f(x)= 
，g(x)=f(2x+1)，则g(－1)等于：
A、3 B、
C、－3 D、－
11、从甲城市到乙城市t分钟的电话费由函数g(t)=1.06×（0.75[t]+1）给出，其中t>0，[t]表示大于或等于t的最小整数，则从甲城市到乙城市5.5分钟的电话费为：
A、5.04元 B、5.56元 C、5.38元 D、5.83元
12、如图，向高为H的水瓶A、B、C、D同时以等速注水，注满为止。
若水深h与注水时间t的函数的图像是右图甲，则水瓶的形状是：
二、填空题：本大题共6小题，每小题4分，共24分，将答案填在各题的相应题号上。
13、对单调增函数定义填空。
一般地，设函数y=f(x)的定义域为A，区间I ①A。如果对于区间I内的 ② 两个值x1,x2，当 x1<x2时，都有 ③ ，那么就说y=f(x)在区间I上是单调增函数，I称为y=f(x)的 ④ 。
x2 (x>0)
14、已知函数f(x)= 2 (x=0) 则f（f(－2)）等于 。
0 (x<0)
15、已知f(x)= 
，则f(x2)= ① ，f（f(x)）= ② .
16、试写出两个函数f(x)与g(x),当它们的定义域均为[－1，2]时，值域均为[1，4]。f(x)= ① ，g (x)= ② 。
17、设A=B=a,b,c,d,e,…,x,y,z(元素为26个英文字母)，作映射f: A
B为：
A=a,b,c,d,e,…,x,y,z
并称A中字母排成的文字为明文，相应的B中对
B=a,b,c,d,e,…,x,y,z
应字母拼成的文字为密文。试破译密文“vnqj vghkd xnt zqd vnqj. rstcx vghkd xnt zqd rstcx. okzx vghkd xnt zqd okzx .” 。
18、下面有五种说法：
（1）奇函数的图像一定经过坐标原点；
（2）若函数的定义域只有一个数，则值域也只有一个数；
（3）若f(x)是奇函数，则f(－1)≠f(1) ；
（4）对应法则和值域分别相同的两个函数是同一函数；
（5）若f(1)－f(－1) >0，f(1)+f(－1) >0，则f(x)一定不是减函数，也不是奇函数。
其中正确的序号是 （注：把你认为正确的都写上）。
三、解答题：本大题共5小题，共66分。
19、（本小题满分12分）
设A=x∣2x2+ax+2=0,B=x∣x2+3x+2a=0,AB=2，
（Ⅰ）求a的值及集合A，B；
（Ⅱ）设全集U=A∪B，求（CUA）
（CUB）；
（Ⅲ）写出（CUA）∪（CUB）的所有子集。
20、（本小题满分12分）
已知f(x)=
的图像经过点（3，3）和（1，－3），
（Ⅰ）求f(x)的解析式；
（Ⅱ）指出f(x)的定义域和值域；
（Ⅲ）作出函数y=f(x)的草图。
21、（本小题满分14分）
已知f(x)为偶函数，当x≥0时，f(x)=x2－2x－3.
(Ⅰ)求函数y=f(x)的表达式并画出它的图像；
(Ⅱ)写出f(x)的单调区间（不要求证明单调性）；
(Ⅲ)指出f(x)的最大值或最小值，并就a的变化，讨论方程f(x)=a(a∈R)的解的个数。
22、（本小题满分14分）
建造一个容积为8m3,深为2m的长方体形无盖水池，如果池底和池壁的造价分别为120元∕m2和80元∕m2。
（Ⅰ）求总造价关于底面一边长的函数解析式，并指出该函数的定义域；
（Ⅱ）试判断（Ⅰ）中的函数在（0，2]和[2，+∞）上的单调性，并用定义加以证明；
（Ⅲ）如何设计水池尺寸，才能使总造价最低？
23、（本小题满分14分）
已知函数f(x)=x2－2x,它的值域为[0，3]，
（Ⅰ）这样的函数有多少个？试举出一例；
（Ⅱ）若f(x)的定义域为[－1，a]∪[2，3]，求a的取值范围；
（Ⅲ）若f(x)的定义域为[－1，a]∪[2，b]，试求a,b应满足的条件。
第一学期月考试卷答题纸
高一 数 学
得分
一、选择题答案
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题：
13、① ② ③ ④
14、
15、① ②
16、① ②
17、
18、
19、
20、
21、
22、
23、