高一年级数学科质量抽检试题
说明: 本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第一卷满分45分, 第Ⅱ卷满分55分,共100分,考试时间100分钟.
第Ⅰ卷(选择题)
一、选择题：（本大题目有15小题，每小题3分，共45分。每小题给出四个选项中，只有一项是符合题目要求的）
1． 已知全集
，集合
，则
为
A．
B． 
C． 
D． 
2． 
的值是
A． 1 B． -1
C．
D．
3． 若角
的终边经过点P（3，-4），则
的值为
A．3/5 B．-4/5 C． -4/3 D．-3/4
4． 化简
的结果为
A．
B．
C． 
D．
5． 已知
，则
的值是
A．1 B．-1 C．1/3 D．-1/3
6． 函数
的图像与函数
的图像的关系为
A.关于X轴对称 B.关于Y轴对称 C.关于直线
对称 D.关于原点对称
7． 在等差数列
中,若
,则
的值为
A. 9 B. 10 C. 18 D. 20
8． 已知
且
∥
,则X的值为
A. -3 B. 3 C. -1/3 D. 1/3
9． 若
,则
的值为
A. 
B. 
C. 
D. 1/2
10．
等于
A. 
B. 
C. 
D. 
11．命题“P或q”为真命题是命题“p且q”为真命题的
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.不充分也不必要条件
12．一个函数的图像按
,平移后得到的图像的解析式为
A.
B.
C.
D.
13．在三角形ABC中,角A,B,C所对的边分别为a,b,c,若a=80,b=100,A=450 ,则此三 角形解的情况为
A. 一解 B. 二解 C. 无解 D. 一解或无解
14．若函数
,在同一周期内,当
时,Y有最大值为3,当
时,Y有最小值为-3,则该函数解析式为
A.
B.
C.
D.
15．某人贷款P元,然后每年等额偿还,10年还清,如果年利率r保持不变,按复利计算,每年应还
A. 
元 B. 
元 C. 
元 D. 
元
第Ⅱ卷(非选择题)
二、填空题：（本大题共4个小题，每小题3分，共12分。把答案填在题中的横线上）
16．
的值为
17．若
都不等于零向量，且
，则
的值为
18．已知点P（4，-9），Q（-2，3），且Y轴与线段PQ的交点为M，则M分
所成的比为
19．在三角形ABC中，角A，B，C所对的边分别为a,b,c, 若三角形ABC的面积为
，则角C的大小是
三、解答题：（本大题共5小题，共43分，解答应写出文字说明、证明过程或演算步骤）
20．如果向量
⑴ 求证：A、B、C三点共线。
⑵ 求
的夹角（用反余弦表示）
21．成等差数列的三个正数的和为15，且这三个数分别加上1，3，9后又成等比数列，
求这三个数。
22． 已知
，求
的值。
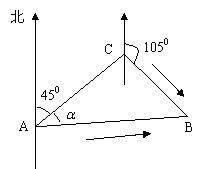
23． 一缉私艇发现在方位角（从正北方向顺时针转到目标方向线的水平角）450、距离
15海里的海面上有一走私船正以25海里/小时的速度沿方位角为1050的方向逃窜。
若缉私艇的速度为35海里/小时，缉私艇沿方位角为450+的方向追去，若要在最
短时间内追上该走私船，求角的正弦值和追上该走私船所需的时间。
 |
24． 已知函数
的定义域为R，任意
，都满足
,
当
⑴判断函数的奇偶性和单调性。
⑵是否存在这样的实数m ，使得当
时，
对所有
均成立，如果存在，求出m的取值范围；如果不存在，说明理由