高一年级数学期中考试试卷2
班级_____________姓名______________分数________________
第一卷
一．选择题（12×4分，每题4分。在每小题的四个选项中，只有一个符合要求。）
1．已知
=（—2 ，—5）的起点为（—1 ，—2），则它的终点为（ ）
A （—3 ，3） B （—1 ，7） C （1 ，—7） D （—2 ，5）
2. 在三角形ABC中，若sinAsinB﹤cosAcosB,则三角形ABC一定是（ ）
A 正三角形 B 直角三角形 C 锐角三角形 D 钝角三角形
3． O是三角形ABC内一点，且
，则O是三角形ABC的（ ）
A 外心 B 内心 C 垂心 D 重心
4． 化简
的结果是（ ）
A cos4
B –cos4 C 
D
5．
若
则
等于（ ）
A 
B 
C 
D
6．
等于 （ ）
A 
B
C
—
D —
7．
的值是（ ）
A 
B
0
C 1
D 2
8．若
，则与
的夹角是（
）
A 
B 
C 
D
或
9．若
，
的最小值是（
）
A 
B
C －1 D 
10．，满足何条件时，等式
成立（ ）
A 与同向 B 与反向 C 与垂直 D 与垂直且模相等．
11．已知点P(cosθ,tanθ)在第三象限，则在区间[0，2π]内的θ的取值范围是（ ）
A (0, 
)
B (, π) C (π, 
) D (, 2π)
12．函数
是（
）
A 最小正周期为2π的奇函数 B 最小正周期为2π的偶函数
C 最小正周期为π的奇函数 D 最小正周期为π的偶函数
第二卷
二．填空题(每题3分，共4小题。12分。把答案填在横线上。)
13．设
∥，则锐角α=___________________
14．设
，若
为偶函数，则t一个可能的取值是___________________.
15．给出下列五个命题：①终边相同的角一定相等。②
③若
，则∥。④函数y=tanx的图象关于点
对称。⑤若k∈R,且
，则k=0或
。其中正确命题是_______________。
16．若对n个向量
存在n个不为0的实数
，使得
成立，则称向量为线形相关。则使得
线形相关的实数
依次可以取_________________。（写出一组即可，不必考虑所有情况。）
三．解答题。（共6小题，60分。解答时写出文字说明，或演算步骤。）
17．设
，
求① sin(α-
)和cos(
)的值。
②
的值。
18．已知
是两个不共线的向量，且
①求证：
和
垂直。
②若
，求sinα的值。
19．已知
=（3，—4），
=（6，—3），
①若A,B,C三点共线，求实数m满足的条件。
②当m 为何值时，三角形ABC是以A为直角顶点的直角三角形。
20．设向量
满足
的夹角为，若向量
的夹角为锐角，
①求
。
②求实数t的取值范围。
21．某体育馆拟用运动场的边角地建一个矩形的健身室。如图，ABCD是一块长为50米的正方形地皮。扇形CEF是运动场的部分，其半径为40米。矩形AGHM就是拟建的健身室。其中G,M分别在AB和AD上，H在弧EF上。设矩形AGHM的面积为S，∠HCF=θ（
），请将S表示为θ的函数，并指出当点H在弧EF的何处时，该健身室的面积最大。
 |
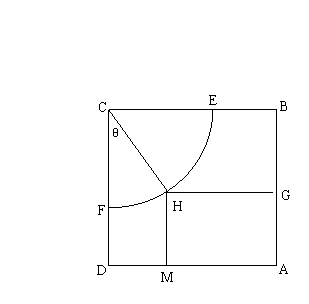22．已知函数
，（a，b为常数，且a<0）的图象过点
，且函数
的最大值为2。
①求函数的解析式，并写出其单调递增区间。
②若函数按向量
作移动距离最小的平移后，使所得的图象关于y轴对称，求向量
的坐标以及平移后的图象对应的函数解析式。