高一年级数学期中形成性阶段检测试卷
学校__________班级_________姓名_______________成绩__________
一．选择题：（12×3=36分）
1．设集合
，则
中的元素个数是（ ）
（A）11 （B）10 （C）16 （D）15
2．下列判断正确的个数为（ ）
⑴
或
是正确的
⑵命题
且
为真
⑶
说法是不正确的
⑷原命题为假，则它的否命题不一定为真
（A）0 （B）1 （C）2 （D）3
3．函数
的反函数是（ ）
（A）
（B）
（C）
（D）
4．定义在R上的函数
对任意两个不等实数a、b，总有
成立，则必有（ ）
（A）函数是奇函数 （B）函数是偶函数
（C）在R上是增函数 （D）在R上是减函数
5．已知
，则函数的解析式为（ ）
（A）
（B）
（C）
（D）
6．已知集合
，下列各式中，不表示从M到N的映射的是（ ）
（A）
（B）
（C）
（D）
7．已知函数
的定义域为
，则在同一坐标系中，函数的图象与直线
的交点个数为（ ）
（A）0个 （B）1个 （C）2个 （D）0个或1个均有可能
8．已知奇函数
的解集为
的解集为
，则
的解集为（ ）（其中
）
（A） （B）
（C）
（D）
9．已知
，则
p是q的（ ）
（A）充分而不必要条件 （B）必要而不充分条件
（C）充要条件 （D）既不充分也不必要条件
10．设是R上的偶函数，并且在
上是减函数，若
，且
，则（ ）
（A）
（B）
（C）
（D）
与
的大小关系不确定
11．已知函数
，若
恒成立，则（ ）
（A）
（B）
（C）
（D）
12．若函数是定义在
上的增函数，且对一切
满足
，则不等式
的解为（ ）
（A）
（B）
（C）
（D）
二．填空题：
13．已知
，且存在反函数，则
=____________________．
14．若函数
的定义域是
，则函数
的定义域是________．
15．已知函数
在
上是减函数，则a的取值范围是_____________．
16．命题“若a>b，则
（a，b，c是实数）”与它的逆命题，否命题，逆否命题四个命题中，真命题的个数为___________个．
17．已知函数
，
都是奇函数，其中
在
内有最大值10，那么在
内的最小值为__________________．
18．已知
，且
，则
的最小值等于________________．
三．计算题：
19．已知函数
，求方程
的解集．
20．已知
且
，求
的取值构成的集合．
21．已知函数
（其中
，a为正实数）
（1）试讨论在上的单调性，并予以证明．
（2）若在
上的值域是，且
，求a的取值范围和相应的m、n的值．
22．设函数对于任意
，都有
，且
时
，
．
（1）求证：是奇函数．
（2）判断的单调性并证明．
（3）试问在
时是否有最值？若有，求出最值；如果没有，说出理由．
（4）解关于x的不等式
．
高一年级期中形成性阶段检测
数学试卷答案
一．选择题
1．A={x∣x∈z 且-10≤x≤-1} B={x∣x∈z 且-5≤x≤5}
∴Card(A∪B)=10+6=16 C
2．（1）“x2≠y2”
x≠y且x≠-y (×)
(2) P假
q真 p且q为假 (×)
（3）逆否命题“x≠-y
x2≠y2”假 （√） （4）
（√）
C
3．y=-x2+1,x∈(-2,0],则y∈(-3,1]
-(y-1)=x2 (x∈(-2,0])
D
4．
C
5．令
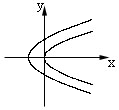
C
6．
B
7．由函数定义可知：非空数集A到B的映射 注：考虑x=7,x=a B
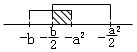
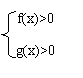8．f(x).g(x)>0
或
|
|
|
或
 |
|
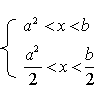
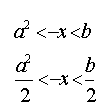
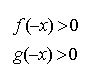
C
9．
∵
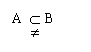A
10．
A
11．
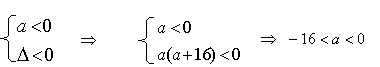
综上可知：
C
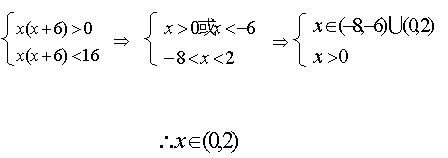
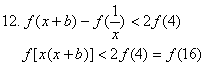
C
二．13．（利用互为反函数的两函数之间关系）
f-1(1)就相当于求x=1时，x2+3x+2=6 ∴f-1(1)=6
14．y=-f(x) x∈[-2,4]
则g(x)=f(x)+f(-x)
|
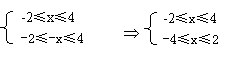
15．
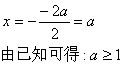
16．原命题：“若a>b,则ac2>bc2（a,b,c∈R）” 假 （c=0）
逆命题：“若ac2>bc2,则a>b”真
∴四个命题中真命题个数为2个
）
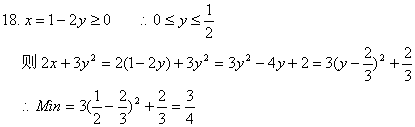
20．A={x∣x2-3x+2=0}={1,2} 且A∪B=A ∴B
A
10.B=φ 即△=a2-4×2×2<0 ∴a∈(-4,4)
20.B≠ф 即△≥0 ∴a≥4或a≤-4
此时，B有可能是{1}，{2}，{1，2}，而由韦达定理知：1≠4 1≠2
∴B不可能是{2}，{1，2} ∴B只能为{1}
将x=1代入后，得a=4
综上可知：符合题意的a∈(-4,4]
21．（1）证明：
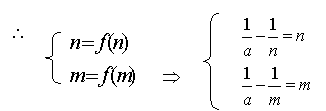（2）
∴m,n 为一元二次方程，ax2-x+a=0的两个不等实根（a>0）
△=1-4a2>0
∴
故
22．（1）
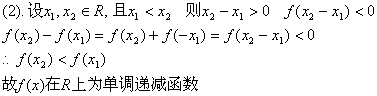
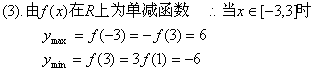
10 
20 
30 
40 
50 