第一学期
高一期中数学考试试卷
(时间：120分钟 总分：150分)
一、选择题：本大题共12小题，每小题5分，共60分．请将每题唯一正确结论的代号填入题后的括号内．
1．如果S={1，2，3，4，5}，M={1，3，4}，N={2，4，5}，
那么（CSM）
（CSN）=（
）
A. {1，3} B、{4} C、{2，5} D、φ
2. 若函数y=
的反函数是
,
(
) 则
等于（ ）
A．
B. 
C 
D 
3. 当命题“若p则q”为真时，下列命题中一定正确的是（ ）
A．若q则p B. 若非p则非q
C. 若非q则非p
D. p且q
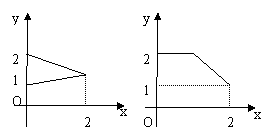
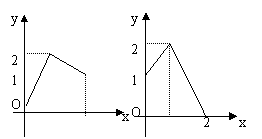4.
设集合
，在下图中能表示从集合A到集合B的映射的是( )
 | |||||
 | |||||
| |||||
| |||||
A. B. C. D.
5. 若一次函数y=kx+b在(-
,+)上是减函数，则点(k,b)在直角坐标平面的（ ）
A. 上半平面 B. 下半平面 C. 左半平面 D. 右半平面
6. 函数①
②
③
④
，其中定义域与值域相同的函数有( )
A． 4个 B. 3个 C. 2个 D. 1个
7.
若函数满足
，则的解析式在下列四式中只有可能是( )
A..
B..
C.. 
D..
8.
已知函数
，则有（ ）
A. 
B. 
C.
D.
9. “(a+b)(b+c)(c+a)=0”的含义是（ ）
A.. a、b、c 两两互为相反数
B.. a、b、c中至少有两个互为相反数
C. a、b、c中有两个为0
D.. a、b、c中至少有一个不为0
10. 函数
的值域是（ ）
A.[0.4] B.[--4,0] C.[-4,4] D.(--4,4)
11. 关于
的方程 
至少有一个负实根的充要条件是（ ）
A.. 
B.. 
C.. 
D.. 
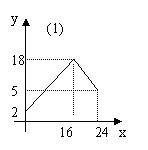
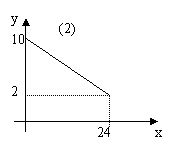12.
下图中的（1），(2)分别表示函数
和的图像，若函数
，则当函数
取得最大值时相应的x值为 ( )
A.. 8 B.. 14 C. 16 D.. 20
二、填空题：本大题共4小题，每小题4分，共16分. 把答案填在题中横线上
13.
=
14.不等式
恒成立，则实数的取值范围是
15求函数
的单调递减区间
16朱老师给出一个函数y=，四个学生甲、乙、丙、丁各指出这个函数的一个性质：
甲：对于 
都有
乙：在
上为减函数
丙：在
上为增函数
丁：
不是函数的最小值
现已知其中恰有三个说法是正确的，则这个函数可能是
（只需写出一个这样的函数即可）
三、解答题：本大题共5小题，共74分. 解答应写出文字说明 , 证明过程或演算步骤.
17．(12分)已知全集U＝{xx
-7x+10
0}，A={xx-4>2} ，B={x
0}
求 （1）C
A (2) AB (3)
(CA) ( C
B).
18．．(12分)已知
，求
（1）的反函数 （2）使
的实数的值
19 (12分)试判断函数f(x)=x+
在区间(0,1) 上的单调性. 并用函数单调性定义证明你的结论。
20．已知函数
在区间[0，1]上有最大值2，求实数m的值(12分)
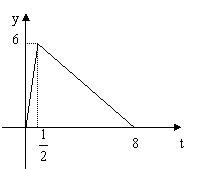21．(12分)某医药研究所开发一种新药，如果成人按规定的剂量服用，据监测，服药后每毫升血液中的
含药量y（
）与时间t（小时）之间
近视满足如图所示的曲线。
(1) 写出服药后y与t之间的函数关系式
(2) 据测定，每毫升血液中含药量不少于
4时治疗疾病有效。假定某病人一天中第
一次服药为7：00，那么一天中怎样安排服药时间、次数效果最佳。
22．(14分) 已知二次函数
及一次函数
（
）若
。
(1) 证明：的图像与的图像一定有两个交点
(2) 试用反证法证明：
(3) 若的图像与的图像的两个交点为A、B，试求出
的取值范围。
答案:
一、选择题
1．D 2. A 3.C 4. D 5. C 6. B 7. D 8. D 9.B 10.C 11.C 12. B
二、填空题
13． 14.5 14.
15.[--1,1] 16.y=x—1 (
…)
三、解答题
17．解：
2
4
6
8
10
12
18.解：(1)
，(3—y)x=ay—1
2
, y
3
4
互换x,y得：
6
(1)
由 得
，（3x+1）(3—x)=(ax—1)(x+a)
9
上是恒成立，故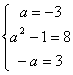 
得a=--3
12
19．解：减函数
2
任取
则
6
∵
∴
∴
10
∴
∴函数f(x)=x+在区间(0,1) 上为减函数
12
20．解：
2
当m<0时，
解得 m=---1 满足题意 5
当m>1时。
解得 m=-2 满足题意 8
当
时，
即
，解得：m=
均不合题意
11
综上，m=--1或2为所求 12翰林汇
21 解：（1）由题意得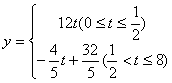
.
5
（2）设第二次服药时在第一次服药后
小时，则
因此第二次服药应在10：00 7
设第三次服药时在第一次服药后
小时，则此时血液中含药量应为两次服药后的含药量的和，则
故第三次服药应在14：00 9
设第四次服药时在第一次服药后
小时（>8）,则此时第一次服进的药已吸收完，此时血液中含药量应为第二、三两次服药后的含药量的和，则
11
故第四次服药应在15：30 12
22．证明：（1）由
得
（*）
∵
。
∴ 
∴ 
∴（*）有两个不相等的实数根即两函数图像一定由两个交点。 4
（2）若结论不成立则
由
∴a+c≤--a ∴--b≤--a 6
∴a≤b 这与条件中a>b矛盾
再由
∴b≤c 这与条件中b>c矛盾 8
综上假设不成立 原不等式成立 9
(3)由条件
为方程（*）的两个根
∴
12
由（2）得
得
14