高一数学同步测试（5）—映射与函数
一、选择题：
1．下列对应是从集合A到集合B的映射的是 （ ）
A．A=R，B={xx＞0且x∈R}，x∈A，f：x→x
B．A=N，B=N＋，x∈A，f：x→x－1
C．A={xx＞0且x∈R}，B=R，x∈A，f：x→x2
D．A=Q，B=Q，f：x→
2．已知映射f:AàB，其中集合A＝{－3，－2，－1，1，2，3，4}，集合B中的元素都是A中的元素在映射f下的象，且对任意的a∈A，在B中和它对应的元素是a，则集合B中的元素的个数是 （ ）
A．4 B．5 C．6 D．7
3．设集合A和B都是自然数集合N，映射f：A→B把集合A中的元素n映射到集合B中的元素2n＋n，则在映射f下，象20的原象是 （ ）
A．2 B．3 C．4 D．5
4．在x克a%的盐水中，加入y克b%的盐水，浓度变成c%(a,b>0,a≠b)，则x与y的函数关系式是 （ ）A．y=
x B．y=
x
C．y=
x D．y=
x
5．函数y=
的值域是 （ ）
A．(－∞，－1 )∪(－1，＋∞) B．(－∞，1)∪(1，＋∞)
C．(－∞，0 )∪(0，＋∞) D．(－∞，0)∪(1，＋∞)
6．下列各组中，函数f(x)和g(x)的图象相同的是 （ ）
A．f(x)=x，g(x)=(
)2 B．f(x)=1，g(x)=x0
C．f(x)=x，g(x)=
D．f(x)=x，g(x)=
7．函数y=
的定义域为 （ ）
A．{x－1≤x≤1} B．{xx≤－1或x≥1}
C．{x0≤x≤1} D．{－1，1}
8．已知函数f(x)的定义域为［0，1］，则f(x2)的定义域为 （ ）
A．(－1，0) B．[－1，1]
C．(0，1) D．［0，1］
9．设函数f(x)对任意x、y满足f(x＋y)=f(x)＋f(y)，且f(2)=4，则f(－1)的值为 （ ）
A．－2 B．±
C．±1 D．2
10．函数y=2－
的值域是
（ ）
A．[－2，2] B．[1，2] C．[0，2] D．[－
，]
11．若函数y=x2—x—4的定义域为[0，m]，值域为[
，-4]，则m的取值范围是 （ ）
A．
B．[
，4] C．[ ，3] D．[ ，＋∞]
12．已知函数f(
＋1)=x＋1，则函数f(x)的解析式为 （ ）
A．f(x)=x2 B．f(x)=x2＋1(x≥1)
D．f(x)=x2－2x＋2(x≥1) C．f(x)=x2－2x(x≥1)
二、填空题：
13．己知集合A ={1，2，3，k} ，B = {4，7，a4，a2＋3a}，且a∈N*，x∈A，y ∈B，使B 中元素y=3x＋1和A中的元素x对应，则a=__ _， k =__ .
14．若集合M={－1，0，1} ，N={－2，－1，0，1，2}，从M到N的映射满足：对每个x∈M，恒使x＋f(x) 是偶数， 则映射f有__ __个.
15．设f(x－1)=3x－1，则f(x)=__ _______.
16．已知函数f(x)=x2－2x＋2，那么f(1)，f(－1)，f(
)之间的大小关系为 .
三、解答题：
17．（1）若函数y= f(2x＋1)的定义域为[ 1，2 ]，求f (x)的定义域.
（2）已知函数f(x)的定义域为［－
，
］，求函数g(x)=f(3x)＋f(
)的定义域.
18．（1）已f ()=
，求f(x)的解析式.
（2）已知y=f(x)是一次函数，且有f [f(x)]=9x＋8，求此一次函数的解析式.
19．求下列函数的值域：
（1）y=－x2＋x，x∈[1，3 ]
（2）y =
（3）
20．已知函数
(x)=f(x)＋g(x)，其中f(x)是x的正比例函数，g(x)是x的反比例函数，
且(
)=16，(1)=8．
（1）求(x)的解析式，并指出定义域；
（2）求(x)的值域.
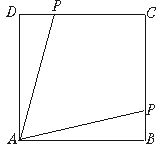
21．如图，动点P从单位正方形ABCD顶点A开始，顺次经B、C、D绕边界一周，当x表示点P的行程，y表示PA之长时，求y关于x的解析式，并求f(
)的值.
22．季节性服装当季节即将来临时，价格呈上升趋势，设某服装开始时定价为10元，并且每周(7天)涨价2元，5周后开始保持20元的价格平稳销售；10周后当季节即将过去时，平均每周削价2元，直到16周末，该服装已不再销售.
（1）试建立价格P与周次t之间的函数关系式.
（2）若此服装每件进价Q与周次t之间的关系为Q＝－0.125(t－8)2＋12，t∈[0，16]，t∈N*，试问该服装第几周每件销售利润L最大?
参考答案
一、选择题： CACBB CDBAC CC
二、填空题：
13.a=2，k=5，14.12
，15.3x＋2，16.f(1)＜f()＜f(－1)
三、解答题：
17.解析：（１）f(2x＋1)的定义域为[1，2]是指x的取值范围是[1，2]，
的定义域为[3，5]
（２）∵f(x)定义域是［－，］∴g(x)中的x须满足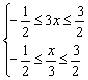
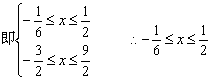∴g(x)的定义域为［－
］.
18.解析：（１）设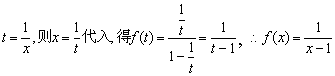
(x≠0且x≠1)
（２）设f(x)=ax＋b，则f[f(x)]=af(x)＋b=a(ax＋b)＋b=a2x＋ab＋b=9x＋8
19．解析：（１）由y=－x2＋x
，∵
．
（２）可采用分离变量法. 
，∵
∴值域为{yy≠1且y∈R.}(此题也可利用反函数来法)
（３）令
(
)，则
，
，
当时，
，∴函数的值域为
．
20．解析： (1)设f(x)=ax，g(x)=
，a、b为比例常数，则(x)=f(x)＋g(x)=ax＋
由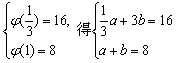
，解得
∴(x)=3x＋
，其定义域为(－∞，0)∪(0，＋∞)
(2)由y =3x＋，得3x2－yx＋5=0(x≠0)
∵x∈R且x≠0，∴Δ=y2－60≥0，∴y≥2
或y≤－2
∴(x) 的值域为(－∞，－2
∪［2，＋∞
21．解析：当P在AB上运动时，y =x，0≤x≤1，
当P在BC上运动时，y=
，1＜x≤2
当P在CD上运动时，y=
，2＜x≤3
当P在DA上运动时，y=4－x，3＜x≤4
∴y=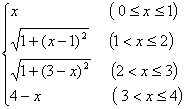
∴f()=
22．解析：
(1)P＝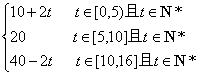 
(2)因每件销售利润＝售价－进价，即L＝P－Q
故有：当t∈[0，5)且t∈N*时，L＝10＋2t＋0.125(t－8)2－12＝
t2＋6
即，当t＝5时，Lmax＝9.125
当t∈[5，10)时t∈N*时，L＝0.125t2－2t＋16
即t＝5时，Lmax＝9.125
当t∈[10，16]时，L＝0.125t2－4t＋36
即t＝10时，Lmax＝8.5
由以上得，该服装第5周每件销售利润L最大.