高一数学同步测试（6）—函数的单调性
一、选择题：
1．在区间(0，＋∞)上不是增函数的函数是 （ ）
A．y=2x＋1 B．y=3x2＋1
C．y=
D．y=2x2＋x＋1
2．函数f(x)=4x2－mx＋5在区间［－2，＋∞］上是增函数，在区间(－∞，－2)上是减函数，则f(1)等于 （ ）
A．－7 B．1
C．17 D．25
3．函数f(x)在区间(－2，3)上是增函数，则y=f(x＋5)的递增区间是 （ ）
A．(3，8) B．(－7，－2)
C．(－2，3) D．(0，5)
4．函数f(x)=
在区间(－2，＋∞)上单调递增，则实数a的取值范围是 （ ）
A．(0，
) B．(
，＋∞)
C．(－2，＋∞) D．(－∞，－1)∪(1，＋∞)
5．已知函数f(x)在区间[a，b]上单调，且f(a)f(b)＜0，则方程f(x)=0在区间[a，b]内（ ）
A．至少有一实根 B．至多有一实根
C．没有实根 D．必有唯一的实根
6．已知函数f(x)=8＋2x－x2，如果g(x)=f( 2－x2 )，那么函数g(x) （ ）
A．在区间(－1，0)上是减函数 B．在区间(0，1)上是减函数
C．在区间(－2，0)上是增函数 D．在区间(0，2)上是增函数
7．已知函数f(x)是R上的增函数，A(0，－1)、B(3，1)是其图象上的两点，那么不等式 f(x＋1)＜1的解集的补集是 （ ）
A．(－1，2) B．(1，4)
C．(－∞，－1)∪[4，＋∞） D．(－∞，－1)∪[2，＋∞）
8．已知定义域为R的函数f(x)在区间(－∞，5)上单调递减，对任意实数t，都有f(5＋t)＝f(5－t)，那么下列式子一定成立的是 （ ）
A．f(－1)＜f(9)＜f(13) B．f(13)＜f(9)＜f(－1)
C．f(9)＜f(－1)＜f(13) D．f(13)＜f(－1)＜f(9)
9．函数
的递增区间依次是 （ ）A．
B．
C．
D
10．已知函数
在区间
上是减函数，则实数
的取值范围是（ ）
A．a≤3 B．a≥－3 C．a≤5 D．a≥3
11．已知f(x)在区间(－∞，＋∞)上是增函数，a、b∈R且a＋b≤0，则下列不等式中正确的是（ ）
A．f(a)＋f(b)≤－f(a)＋f(b)］ B．f(a)＋f(b)≤f(－a)＋f(－b)
C．f(a)＋f(b)≥－f(a)＋f(b)］ D．f(a)＋f(b)≥f(－a)＋f(－b)
12．定义在R上的函数y=f(x)在(－∞，2)上是增函数，且y=f(x＋2)图象的对称轴是x=0，则 （ ）
A．f(－1)＜f(3) B．f (0)＞f(3) C．f (－1)=f (－3) D．f(2)＜f(3)
二、填空题：
13．函数y=(x－1)-2的减区间是___ _．
14．函数y=x－2
＋2的值域为__
___．
15、设
是
上的减函数，则
的单调递减区间为 .
16、函数f(x) = ax2＋4(a＋1)x－3在[2，＋∞]上递减，则a的取值范围是__ ．
三、解答题：
17．f(x)是定义在( 0，＋∞)上的增函数，且f(
) = f(x)－f(y)
（1）求f(1)的值．
（2）若f(6)= 1，解不等式 f( x＋3 )－f(
) ＜2 ．
18．函数f(x)=－x3＋1在R上是否具有单调性？如果具有单调性，它在R上是增函数还是减函数？试证明你的结论．
19．试讨论函数f(x)=
在区间［－1，1］上的单调性．
20．设函数f(x)=
－ax，(a＞0)，试确定：当a取什么值时，函数f(x)在0，＋∞)上为单调函数．
21．已知f(x)是定义在(－2，2)上的减函数，并且f(m－1)－f(1－2m)＞0，求实数m的取值范围．
22．已知函数f(x)=
，x∈［1，＋∞］
（1）当a=
时，求函数f(x)的最小值；
（2）若对任意x∈[1，＋∞
，f(x)＞0恒成立，试求实数a的取值范围．
参考答案
一、选择题： CDBBD ADCCA BA
二、填空题：13.
(1，＋∞)， 14. (－∞，3)，15.
， 
三、解答题：17.解析：①在等式中
，则f(1)=0．
②在等式中令x=36，y=6则
故原不等式为：
即f[x(x＋3)]＜f(36)，
又f(x)在(0，＋∞)上为增函数，
故不等式等价于：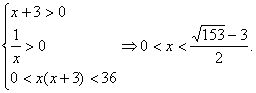
18.解析： f(x)在R上具有单调性，且是单调减函数，证明如下：
设x1、x2∈(－∞，＋∞)， x1＜x2 ，则f(x1)=－x13＋1， f(x2)=－x23＋1．
f(x1)－f(x2)=x23－x13=(x2－x1)(x12＋x1x2＋x22)=(x2－x1)［(x1＋
)2＋
x22］．
∵x1＜x2，∴x2－x1＞0而(x1＋)2＋x22＞0，∴f(x1)＞f(x2)．
∴函数f(x)=－x3＋1在(－∞，＋∞)上是减函数．
19.解析： 设x1、x2∈－1，1］且x1＜x2，即－1≤x1＜x2≤1．
f(x1)－f(x2)=
－
=
=
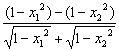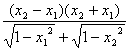
∵x2－x1＞0，
＞0，∴当x1＞0，x2＞0时，x1＋x2＞0，那么f(x1)＞f(x2)．
当x1＜0，x2＜0时，x1＋x2＜0，那么f(x1)＜f(x2)．
故f(x)=在区间［－1，0］上是增函数，f(x)=在区间［0，1］上是减函数．
20.解析：任取x1、x2∈0，＋
且x1＜x2，则
f(x1)－f(x2)=
－
－a(x1－x2)=
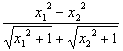－a(x1－x2)
=(x1－x2)(
－a)
(1)当a≥1时，∵＜1，
又∵x1－x2＜0，∴f(x1)－f(x2)＞0，即f(x1)＞f(x2)
∴a≥1时，函数f(x)在区间［0，＋∞)上为减函数．
(2)当0＜a＜1时，在区间［0，＋∞］上存在x1=0，x2=
，满足f(x1)=f(x2)=1
∴0＜a＜1时，f(x)在［０，＋上不是单调函数
注： ①判断单调性常规思路为定义法；
②变形过程中
＜1利用了
＞x1≥x1;＞x2；
③从a的范围看还须讨论0＜a＜1时f(x)的单调性，这也是数学严谨性的体现．
21.解析： ∵f(x)在(－2，2)上是减函数
∴由f(m－1)－f(1－2m)＞0，得f(m－1)＞f(1－2m)
∴
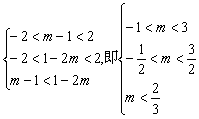解得
，∴m的取值范围是(－
)
22.解析： (1)当a=时，f(x)=x＋
＋2，x∈1，＋∞)
设x2＞x1≥1，则f(x2)－f(x1)=x2＋
=(x2－x1)＋
=(x2－x1)(1－
)
∵x2＞x1≥1，∴x2－x1＞0，1－＞0，则f(x2)＞f(x1)
可知f(x)在［1，＋∞)上是增函数．∴f(x)在区间［1，＋∞上的最小值为f(1)=
．
(2)在区间［1，＋∞上，f(x)=＞0恒成立
x2＋2x＋a＞0恒成立
设y=x2＋2x＋a，x∈1，＋∞)，由y=(x＋1)2＋a－1可知其在[1，＋∞)上是增函数，
当x=1时，ymin=3＋a，于是当且仅当ymin=3＋a＞0时函数f(x)＞0恒成立．故a＞－3．