高一数学同步测试（7）—反函数
一、选择题：
1
．设函数f(x)＝1－
(－1≤x≤0)，则函数y＝f－1(x)的图象是 （ ）
A.
y B. y 1 C. y D.
y 1
1
x
1
O
x
－1
－1
－1 O x
O
1 x
2．函数y=1－
(x≥1)的反函数是 （ ）
A．y=(x－1)2＋1，x∈R B．y=(x－1)2－1，x∈R
C．y=(x－1)2＋1，x≤1 D．y=(x－1)2－1，x≤1
3．若f(x－1)= x2－2x＋3 (x ≤1)，则f－1(4)等于 （ ）
A．
B．1－ C．－ D．－2
4．与函数y=f(x)的反函数图象关于原点对称的图象所对应的函数是 （ ）
A．y=－f(x) B．y= f-1(x) C．y =－f-1(x) D．y =－f-1(－x)
5．设函数
，则
的定义域为 （ ）
A．
B．
C．
D．
6．若函数
的反函数是
，
，则
等于 （ ）
A．
B．
C．
D．
7．已知函数
的反函数就是
本身，则的值为
（ ）
A．
B．1
C．3
D．
8．若函数存在反函数，则方程
（ ）
A．有且只有一个实数根 B．至少有一个实数根
C．至多有一个实数根 D．没有实数根
9．函数f(x)=－
·
(x≤－1)的反函数的定义域为 （ ）
A．(－∞，0］ B．(－∞，＋∞)
C．(－1，1) D．(－∞，－1)∪(1，＋∞)
10．若函数f(x)的图象经过点(0，－1)，则函数f(x＋4)的反函数的图象必经过点 （ ）
A．(－1，4) B．(－4，－1) C．(－1，－4) D．(1，－4)
11．函数f(x)＝
(x≠0)的反函数f－1(x)＝ （ ）
A．x(x≠0) B． (x≠0) C．－x(x≠0) D．－ (x≠0)
12、点(2，1)既在函数f(x)=
的图象上，又在它的反函数的图象上，则适合条件的数组(a，b)有 （ ）
A．1组 B．2组 C．3组 D．4组
二、填空题：
13．若函数f(x)存在反函数f－1(x)，则f－1[f(x)]=___ ； f[f－1(x)]=___ __．
14．已知函数y＝f(x)的反函数为f－1(x)＝
－1(x≥0)，那么函数f(x)的定义域为__ _．
15．设f(x)=x2－1(x≤－2)，则f－1(4)=__ ________．
16．已知f(x)＝f－1(x)＝
(x≠－m)，则实数m =
．
三、解答题：
17．（1）已知f(x) = 4x－2x＋1 ，求f－1(0)的值．
（2）设函数y= f(x)满足 f(x－1) = x2－2x＋3 (x ≤ 0)，求 f－1(x＋1)．
18．判断下列函数是否有反函数，如有反函数，则求出它的反函数．
（1）
；
（2）
．
（3）
19．已知f(x)=
（1）求y=f(x)的反函数 y= f－1 (x)的值域;
（2）若(2，7)是 y = f－1 (x)的图象上一点，求y=f(x)的值域．
20．已知函数
，
（1）求
及其
；
（2）求
的反函数．
21．己知
(x≥1)，
（1）求的反函数，并求出反函数的定义域；
（2）判断并证明的单调性．
22．给定实数a，a≠0，且a≠1，设函数
．试证明：这个函数的图象关于直线y=x成轴对称图形．
参考答案
一、选择题： DCCDD ACCAC BA
二、填空题：13.x，x，14.x≥－1，15.－
，16.m＝－2
三、解答题：
17.解析：（１）设f－1(0)=a，即反函数过(0，a)， ∴原函数过(a，0)．
代入得 ：0=4a－2a＋1 ，2a(2a－2)=0，得a=1，∴f 
=1．
（２）先求f(x)的反函数
．
18.解析：⑴令
得到对应的两根：
这说明函数确定的映射不是一一映射，因而它没有反函数．
⑵由
，得
∵
，∴ 
，
互换
得
又由的值域可得反函数定义域为
∴反函数为
．
⑶由
得其反函数为
；
又由
得其反函数为
．
综上可得，所求的反函数为
．
注：求函数
的反函数的一般步骤是：
⑴反解，由解出
，写出
的取值范围；
⑵互换，得
；
⑶写出完整结论(一定要有反函数的定义域)．
⑷求分段函数的反函数，应分段逐一求解；分段函数的反函数也是分段函数．
19.解析：
（１）反函数的定义域、值域分别是原函数的值域、定义域．∴反函数的值域为{yy
}
（２）∵(2，7)是y=f－1(x)的图象上一点，∴(7，2)是y=f(x)上一点．
∴
∴f(x)的值域为{yy≠2}．
20．解析：⑴∵
，
∴
，其值域为
，
又由
得
，
∴
，
∴
．
⑵由
，解得
∴的反函数为
．
说明：
并不是的反函数，而是
的反函数．
题中有的形式，我们先求出，才能求出．
21.解析：⑴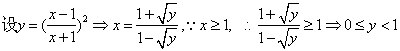
，
即的定义域为
；
⑵设
，
，即在
上单调递增．
22、证法一:
……①
由①式得
……②
由此得a=1，与已知矛盾，
又由②式得
这说明点P′（y′,x′）在已知函数的图象上，因此，这个函数的图象关于直线y=x成轴对称图形.
证法二:先求所给函数的反函数:由
得 y(ax－1)=x－1，
即 (ay－1)x=y－1．
即 ax－a=ax－1，
由此得a=1，与已知矛盾，所以ay－1≠0．
因此得到
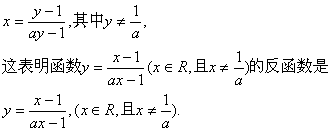
由于函数y=f(x)的图象和它的反函数y=f－1(x)的图象关于直线y=x对称，所以函数
的图象关于直线y=x成轴对称图形.