上学期
高一数学同步测试（8）—指数与指数函数
一、选择题：
1．化简［3
］
的结果为 （ ）
A．5 B．
C．－ D．－5
2．化简
的结果为 （ ）
A．a16 B．a8 C．a4 D．a2
3．设函数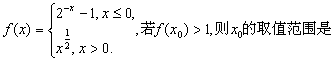
（ ）
A．(－1，1) B．(－1，＋
)
C．
D．
4．设
，则 （ ）
A．y3＞y1＞y2 B．y2＞y1＞y3 C．y1＞y2＞y3 D．y1＞y3＞y2
5．当x∈［－2，2
时，y=3－x－1的值域是 （ ）
A．［－
，8］ B．［－，8］ C．(
，9) D．［，9］
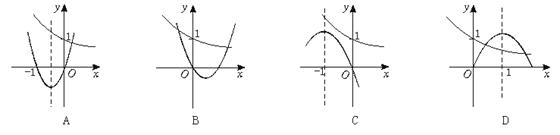
6．在下列图象中，二次函数y=ax2＋bx＋c与函数y=(
)x的图象可能是 （ ）
7．已知函数f(x)的定义域是(0，1)，那么f(2x)的定义域是 （ ）
A．(0，1) B．(
，1) C．(－∞，0) D．(0，＋∞)
8．若
，则
等于 （ ）
A．2
－1 B．2－2 C．2＋1 D． ＋1
9．设f(x)满足f(x)＝f(4－x)，且当x＞2 时f(x)是增函数，则a＝f(1.10.9)，b= f(0.91.1)，c＝
的大小关系是 （ ）
A．a＞b＞c B．b＞a＞c C．a＞c＞b D．c＞b＞a
10．若集合
，则M∩P= （ ）
A．
B．
C．
D．
11．若集合S＝{yy＝3x，x∈R}，T＝{yy＝x2－1，x∈R}，则S∩T是 （ ）
A．S B．T C．
D．有限集
12．下列说法中，正确的是 （ ）
①任取x∈R都有3x＞2x
②当a＞1时，任取x∈R都有ax＞a－x
③y=(
)－x是增函数
④y=2x的最小值为1
⑤在同一坐标系中，y=2x与y=2－x的图象对称于y轴
A．①②④ B．④⑤ C．②③④ D．①⑤
二、填空题：
13．计算：
＝ ．
14．函数
在
上的最大值与最小值的和为3，则
．
15．函数y=
的值域是_
_______．
16．不等式
的解集是
．
三、解答题：
17．已知函数f(x)=ax＋b的图象过点(1，3)，且它的反函数f－1(x)的图象过(2，0)点，试确定f(x)的解析式．
18．已知
求
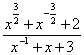的值．
19．求函数y=3
的定义域、值域和单调区间．
20．若函数y=a2x＋b＋1(a＞0且a≠1，b为实数)的图象恒过定点(1，2)，求b的值．
21．设0≤x≤2，求函数y=
的最大值和最小值．
22．设
是实数，
，试证明：对于任意
在
上为增函数．
参考答案
一、选择题： BCDDA ACADC AB
二、填空题：13.
，14.2，15. (0，1) ，16.
．
三、解答题：
17.解析： 由已知f(1)=3，即a＋b=3 ①
又反函数f－1(x)的图象过(2，0)点即f(x)的图象过(0，2)点．
即f(0)=2 ∴1＋b=2
∴b=1代入①可得a=2
因此f(x)=2x＋1
18.解析：由
可得x＋x－1=7
∵
∴
=27
∴
=18，
故原式=2
19.解析：(1)定义域显然为(－∞，＋∞)．
(2)
是u的增函数，
当x=1时，ymax=f(1)=81，而y=
＞0．
∴
．
(3) 当x≤1 时，u=f(x)为增函数， 
是u的增函数，
由x↑→u↑→y↑
∴即原函数单调增区间为(－∞，1］；
当x＞1时，u=f(x)为减函数，是u的增函数，
由x↑→u↓→y↓
∴即原函数单调减区间为［1，＋∞.
20.解析：∵x=－
时，y=a0＋1=2
∴y=a2x＋b＋1的图象恒过定点(－，2)
∴－=1，即b=－2
21.解析：设2x=t，∵０≤x≤2，∴1≤t≤4
原式化为：y=(t－a)2＋1
当a≤1时，ymin=
；
当1＜a≤
时，ymin=1，ymax=
；
当a≥4时，ymin=
．
22.证明：设
，则
，
由于指数函数
在上是增函数，且
，所以
即
，
又由
，得
，
，∴
即
，
所以，对于任意在上为增函数．