高一数学同步测试（10）—函数单元测试
一、选择题：(本题共12题，每小题5分，满分60分)
1．若a、b、c∈R＋，则3a=4b=6c，则 （ ）
A．
B．
C．
D．
2．集合
，映射
，使任意
，都有
是奇数，则这样的映射共有 （ ）
A．60个 B．45个 C．27个 D．11个
3．已知
的反函数
－1(x)的图像的对称中心是(—1，3)，则实数a等于 （ ）
A．2 B．3 C．－2 D．－4
4．已知
，其中
，则下列不等式成立的是 （ ）
A．
B．
C．
D．
5．函数f(x)=
＋2 (x≥1)的反函数是 （ ）
A．y=(x－2)2＋1 (x∈R) B．x=(y－2)2＋1 (x∈R)
C．y=(x－2)2＋1 (x≥2) D．y=(x－2)2＋1 (x≥1)
6．函数y=lg(x2－3x＋2)的定义域为F，y=lg(x－1)＋lg(x－2)的定义域为G，那么 （ ）
A．F∩G=
B．F=G
C．F 
G D．G F
7．已知函数y=f(2x)的定义域是[－1，1]，则函数y=f(log2x)的定义域是 （ ）
A．(0，＋∞) B．(0，1)
C．[1，2] D．[
，4]
8．若
≥
，则 （ ）
A．
≥0 B．
≥0 C．≤0
D．≤0
9．函数
是单调函数的充要条件是 （ ）
A．
B．
C．
D．
10．函数
的递增区间依次是 （ ）
A．
B．
C．
D
11．将进货单价为80元的商品按90元一个出售时，能卖出400个，根据经验，该商品若每个涨(降)1元，其销售量就减少(增加)20个，为获得最大利润，售价应定为 （ ）
A．92元 B．94元 C．95元 D．88元
12．某企业2002年的产值为125万元，计划从2003年起平均每年比上一年增长20%，问哪一年这个企业的产值可达到216万元 （ ）
A．2004年 B．2005年 C．2006年 D．2007年
二、填空题：(本题共4小题，每小题4分，满分16分)
13．函数
[
]图象与其反函数图象的交点坐标为 ．
14．若
且
，则
的取值范围是 ．
15．lg25＋
lg8＋lg5·lg20＋lg22=
．
16．已知函数
，那么
____________．
三、解答题：(本题共6小题，满分74分)
17．(本题满分12分)
设A＝｛x∈R｜2≤ x ≤ π｝，定义在集合A上的函数y=logax (a＞0，a≠1)的最大值比最小值大1，求a的值．
18．(本题满分12分)
已知f(x)=x2＋(2＋lga)x＋lgb，f(－1)=－2且f(x)≥2x恒成立，求a、b的值．
19．(本题满分12分)
“依法纳税是每个公民应尽的义务”，国家征收个人工资、薪金所得税是分段计算的：总收入不超过800元的，免征个人工资、薪金所得税；超过800元部分需征税，设纳税所得额(所得额指月工资、薪金中应纳税的部分)为x，x=全月总收入－800(元)，税率见下表：
| 级数 | 全月应纳税所得额x | 税率 |
| 1 | 不超过500元部分 | 5% |
| 2 | 超过500元至2000元部分 | 10% |
| 3 | 超过2000元至5000元部分 | 15% |
| … | … | … |
| 9 | 超过100000元部分 | 45% |
（1）若应纳税额为f(x)，试用分段函数表示1~3级纳税额f(x)的计算公式；
（2）某人2004年10月份工资总收入为4000元，试计算这个人10月份应纳个人所得税多少元？
20．(本题满分12分)
设函数f(x) =
＋lg
．
（1）试判断函数f(x)的单调性 ，并给出证明；
（2）若f(x)的反函数为f－1 (x) ，证明方程f－1 (x)= 0有唯一解．
21．(本题满分13分)
某地区上年度电价为0.80元/kW· h，年用电量为a kW· h．本年度计划将电价降到0.55元/kW·h至0.75元/kW·h之间，而用户期望电价为0.4元/kW·h．经测算，下调电价后新增的用电量与实际电价和用户期望电价的差成反比(比例系数为k)．该地区电力的成本为0.3元/kW·h．
（1） 写出本年度电价下调后，电力部门的收益y与实际电价x的函数关系式．
（2） 设k=0.2a，当电价最低定为多少时，仍可保证电力部门的收益比上年至少增长20%？ (注：收益=实际用电量×(实际电价－成本价))．
22．(本小题满分13分)
已知
设
P：函数
在R上单调递减．
Q：不等式
的解集为R，如果P和Q有且仅有一个正确，求
的取值范围．
参考答案
一、选择题： BBACC DDBAC CC
二、填空题：13.
，14.
，15.3，16.
三、解答题：(本题共6小题，满分74分)
17.解析： a＞1时，y=logax是增函数，logaπ－loga2＝1，即loga
＝1，得a=．
0＜a＜1时，y=logax是减函数，loga2－logaπ＝1，
即loga
＝1，得a＝．
综上知a的值为或．
18.解析：由f(－1)=－2得：1－(2＋lga)＋lgb=－2
即lgb=lga－1 ①
由f(x)≥2x恒成立，即x2＋(lga)x＋lgb≥0， ∴lg2a－4lgb≤0，
把①代入得，lg2a－4lga＋4≤0，(lga－2)2≤0
∴lga=2，∴a=100，b=10
19.解：(1)依税率表，有
第一段：x·5%
第二段：(x－500)·10%＋500·5%
第三段：(x－2000)·15%＋1500·10%＋500·5%
即：f(x)=
(2)这个人10月份纳税所得额
x=4000－800=3200
f(3200)=0.15(3200－2000)＋175=355(元)
答：这个人10月份应缴纳个人所得税355元．
20.解析：(1)由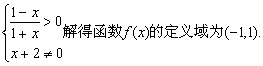
.又∵
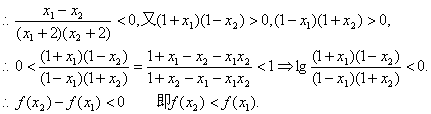
故函数f(x)在区间(－1，1)内是减函数．
(2)这里并不需要先求出f(x)的反函数f－1(x)，再解方程f－1(x)=0
∵
的一个解．
若方程f －1(x)=0还有另一解x0
，则
，这与已知矛盾．
故方程f －1(x)=0有唯一解．
21.解析：(１)设下调后的电价为x元/kW·h，用电量增至(
＋a)
依题意知，y=(
＋a)(x－0.3)，(0.55≤x≤0.75)
(２)依题意有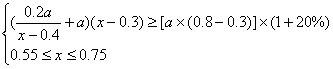
整理得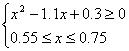
解此不等式得0.60≤x≤0.75
答：当电价最低定为0.60元/kW·h，仍可保证电力部门的收益比去年至少增长20%．
22.解析：函数
在R上单调递减
不等式
∵
