高一数学第一学期期中测试2
数 学 试 卷
（命题、制卷人：刘群建）
第Ⅰ卷（选择题，共30分）
一、 选择题（本大题共12个小题，每小题2.5分，共30分。每小题只有唯一正确答案。）
1、已知A=
，B=
，则A
B等于（ ）
A、R B、
C、
D、
2、若命题p：中国载人航空飞船于2003年10月首次飞行成功，命题q：
，则下列命题中为真命题的是（ ）
A、p且q B、p或q
C、非p D、非p且非q
3、命题“
、
都是偶数，则＋是偶数”的逆否命题是（ ）
A、＋不是偶数，则、都不是偶数
B、＋是偶数，则、都不是偶数
C、＋不是偶数，则、不都是偶数
D、＋是偶数，则、不都是偶数
4、设A、B、C、是三个集合，则“AB=AC”是“B=C”的（ ）条件
A、充分但不必要 B、必要但不充分
C、充分且必要 D、既不充分也不必要
5、函数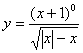
的定义域是（ ）
A、
B、
C、
D、
6、下列四个命题：
① 函数是定义域到值域的映射。
②
是函数
③函数
（
）的图象是一条直线
④函数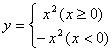
的图象是抛物线
其中正确的命题个数是（ ） A、1 B、2
C、3 D、4
7、在
上为增函数的是（ ）
A、
B、
C、
D、
8、函数
的值域是（ ）
A、
B、
C、R D、
9、如果函数
对于任意实数
都有
，那么（ ）
A、
<
<
B、<<
C、<< D、<<
10、若函数
满足
，当
时
，
则当
时，
=（
）
A、
B、
C、
D、
11、若函数
在区间
上是减函数，则实数的取值
范围是（ ） A、
B、
C、
D、
12、设全集为
，
、
是的两个非空子集，定义与的差集为
，则
等于（ ）
A、
B、
C、
D、
第Ⅱ卷（非选择题，共70分）
二、填空题（本大题共4个小题，每小题4分，共16分）
13、定义域为R的函数的值域为
，则函数
的值域为 。
14、若函数
，则
=
。
15、已知
，
，若
，则的值为
。
16、已知关于
的函数
（
为常数且
），若
（
），则
的值等于
。
三、解答题（本大题共5个小题，共54分，解答应写出文字说明、证明过程或演算步骤）
17、（本小题满分为11 分）已知
，
，
（1） 求
及
（2） 若I=R，求
18、（本小题满分为11 分）若
（
）。求
（1）的表达式、定义域和值域。
（2）
的表达式、定义域和值域。
19、（本小题满分为11 分）作函数=
的图象，指出它的单调区间，并证明在区间
上是增函数。
20、（本小题满分为10分）我国是水资源比较贫乏的国家之一，各地采用价格调控手段来达到节约用水的目的，某市用水收费的方法是：水费=基本费+超额费+损耗费，若每月用水量不超过最低限量 
时，只付基本费8元和每户每月的定额损耗费
元；若用水量超过最低限量 时，除了付同上的基本费和损耗费外，超过部分每付元的超额费，已知每户每月的定额损耗费不超过5元。现该市有一家庭今年第一季度的用水量和支付费用如下表所示：
| 月份 | 用水量 | 水费 |
| 1月 | 9 | 9元 |
| 2月 | 15 | 19元 |
| 3月 | 22 | 33元 |
根据该表格中的数据，求出、、。
21、（本小题满分为11分）定义在R上的函数，
，当时
，且对任意的
有
（1） 求证：
（2） 求证：对任意的
，恒有
（3） 求证：是R上的增函数。
（4） 若
，求的取值范围。
第一学期期中数学试题答卷
二、填空题：（每小题4分，共16分）
13、 ； 14、 ；
15、 ； 16、 ；
三、解答题：
17、(11分)
18、（11分）
19、（11分）
20、（10分）
21、（11分）
第一学期期中测试
数学试卷参考答案及评分标准
一、 选择题（本大题共12个小题，每小题2.5分，共30分。）
1、B 2、B 3、C 4、B 5、C 6、A
7、D 8、B 9、A 10、C 11、B 12、B
二、填空题（本大题共4个小题，每小题4分，共16分）
13、 14、1
15、=1或
16、
三、解答题（本大题共5个小题，共54分，解答应写出文字说明、证明过程或演算步骤）
（3） 17、（本小题满分为11 分）
解：由
得
或
，∴
…………………2分
由
得
， ∴
……………………4分
由
得
， ∴
…………………6分
∴（1）=
……………………………………………7分
=
……………………………………8分
（2）∵I=R，
…………………………………9分
∴
………………………………10分
∴=
…………………………11分
18、（本小题满分为11 分）
解：（1）∵=
∴=
+2…………3分
由得
∴的定义域为
……5分
∵
，∴≥1，+2≥3， ∴的值域为
………7分
（4） 由
==+2得=－2， ∵，∴
………8分
∴的反函数为==
………………………………9分
其定义域为，值域为………………………………11分
19、（本小题满分为11 分）
解：∵= = 
= 
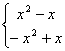
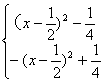
……………2分
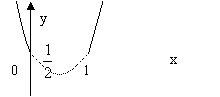
其图象如下：
由图可知，它的单调区间为：
，
，
，
………………6分
下面证明在区间上是增函数。
证明：设
，…………………………………………………………7分
则
－
=（
-
）-（
-
）=（-）-（-）
=（-）（+-1）…………………………………9分
∵，∴->0, +-1>0
∴－>0,即>……………………………………10分
故在区间上是增函数。 ……………………………………11分
20、（本小题满分为10分）
解：设每月的用水量为，支付费用为元。则由题有
……………………………………3分
由
有
………………………………………………4分
由第2、3月的费用都大于13知用水量15、22都大于最低限量，则有
…………………………………………5分
两式相减得
……………6分
∴
……7分
再分析1月份的用水量是否超过最低限度。
不妨设
，将
代入
得
由此有7=9，矛盾。………………………………………………8分
∴
，1月份的付款方式选
∴=9，即
………………………………………………9分
从而
故
……………10分
21、（本小题满分为11分）
（1）证明：设
，则
=
·，∴=
…1分
∵，∴=1 ……………………………………2分
（2）证明：当时>0; 当时
,∴
>0…3分
又
=
==1，∴此时=
>0…4分
当
时，==1>0
∴对任意的，恒有 …………………………5分
（5） 证明:设
，则->0;
∵当时,∴
(-)>1………………………6分
又>0, >0,
=
=(-)>…………7分
∴是R上的增函数。……………………………………8分
(4)解：由得
， ………………9分
由（3）知
………………………………………10分
∴
……………………………………………………11分