高一数学第一学期期中试卷4
命题： 郎建华
一、 选择题（每题3分，共33分）
1、集合
,则M的子集个数为
（ ）
A) 2 B) 3 C) 4 D) 8
2如果集合
那么
（ ）
A) 
B) 
C) 
D) 
3、下列各组函数中，表示同一函数的是 （ ）
4、
（ ）
5、
（ ）
A) – 4 B) –2 C) 1 D) 3
6、已知函数
，若f(a) = 3 ，则a的取值个数为 （ ）
A) 1 B) 2 C) 3 D) 4
7、函数
,给定区间E, 对任意的
当
时，总有
，则下列区间可作为E的是
( )
A) (-3,-1) B) (-1,0) C) (1,2) D) (3,6)
8、如果命题“p或q”与命题“
”都是真命题，那么
( )
A) 命题p是真命题 B) 命题q是真命题
C) 命题q是假命题 D) 命题p与q同真同假
9、已知三个互不相等的实数a,b,c满足：（1）若b不是最大，则a最小 ，（2）若c不是最小，则a最大 ,则这三个数的大小关系是 （ ）
A) c>b>a B) a>b>c C) a>c>b D) b>a>c
10、已知函数
且函数
的图象关于直线
对称，则
的值等于
（ ）
A) 
B) 
C)
–1
D) –2
11、已知两个命题， 即
小于1的正根， 则p成立是q成立的
(
)
A)充分不必要条件 B)必要不充分条件
C)充要条件 D)既不充分也不必要条件
二、 填空题（每题3分，共18分）
|
|
A U,且A={ 2a-1 ,2 }, 
则 a=______________；
13、函数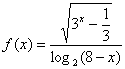
的定义域是__________________;
14、函数
的值域是_________________；
15、函数
在区间
上单调递增，则a的取值范围是____________；
16、已知定义在上R的二次函数
的值域为
，且
，则
17、命题 “对任意的实数x, 不等式
成立，则
”的否命题是_________________________________________________________。
三、 解答题 （共6题，共49分）
18、已知R为全集，
, 求 
。（7分）
19、证明函数
在其定义域上是减函数。 （7分）
20、已知函数
（1） 作出这个函数的图象；
（2） 
（8分）
21、已知命题p：
是R上的减函数；
命题q：
函数
的值域为R.。
若
求实数a的取值范围。
(8分)
22、某商店将进货每个10 元的商品按每个18元出售时，每天可卖出60个。商店经理到市场上做了一番调查后发现，若将这种商品的售价（在每个18元的基础上）每提高1元，则日销售量就减少5个；若将这种商品的售价（在每个18元的基础上）每降低1元，则日销售量就增加10个。为获取每日最大利润，此商店的售价应为每个多少元？ （9分）
现给出两个函数和一个区间如下：
；
（1）
(2) 
(10分)