第十六教时
教材：续第十五教时 《教学与测试》第74、75课
目的：同第十五教时
过程：
一、处理《教学与测试》第74、75课 （略）
二、 补充例题（视教学情况选用）：
1．a、b为非零向量，当a + tb(tÎR)的模取最小值时，
1°求t的值 2°求证：b与a + tb垂直
解：1° a + tb2 = a2 + t2b2 + 2tab
∴当t =
时, a
+ tb最小
2° ∵b•(a + tb) = a•b - 
= 0 ∴b与a + tb垂直
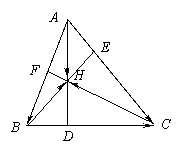
2．如图，AD、BE、CF是△ABC的三条高，
求证：AD、BE、CF相交于一点。
证：设BE、CF交于一点H，
= a, 
= b, 
= h,
则
= h - a
, 
= h - b
, 
= b - a
∵^, ^
∴
∴^
又∵点D在AH的延长线上，∴AD、BE、CF相交于一点
3．
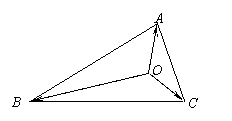已知O为△ABC所在平面内一点，且满足
2 + 2 = 
2 + 
2 = 
2 + 2，
求证：^
证：设= a, = b, = c,
则= c - b,
= a - c,
= b - a
由题设：2 +2 =2 +2 =2 +2，
化简：a2 + (c - b)2 = b2 + (a - c)2 = c2 + (b - a)2
得： c•b = a•c = b•a
从而•= (b - a)•c = b•c - a•c = 0
∴^ 同理：^, ^
三、作业： 《教学与测试》P156 4—9
P158 4—7