高一数学期中测试题3
一、选择题：(本大题共12小题，每小题5分， 共60分)
1．如图，I是全集，M、P、S是I的3个子集，则阴影部分所表示的集合是 （ ）
A．(M∩P)∩S
B．(M∩P)∪S
C．(M∩P)∩
D．(M∩P)∪
2．已知集合M={(x，y)x＋y=2}，N={(x，y)x－y=4}，那么集合M∩N为 （ ）
A．x=3，y=－1 B．(3，－1) C．{3，－1} D．{(3，－1)}
3．不等式
的解集是 （ ）
A．
B．
C．{
} D．
4．设A={x－1≤x＜2＝，
B= {xx＜a＝，若A∩B≠
，则a的取值范围是 （ ）
A．a ＜ 2 B．a ＞－2 C．a ＞－1 D．－1＜a≤2
5．“p或q是假命题”是“非p为真命题”的 （ ）
A．充分而不必要条件 B．必要而不充分条件
C．充要条件 D．既不充分也不必要条件
6．集体
的子集个数是 （ ）
A.32 B.31 C.16 D.15
7．设函数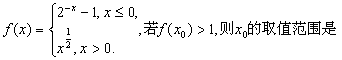
（ ）
A．(－1，1) B．(－1，＋
)
C．
D．
8．若集合
（ ）
A．
B．
C．
D．
9．已知(2，1)在函数f(x)=
的图象上，又知f－1
=1，则f(x)等于 （ ）
A．
B．
C．
D．
10．函数f(x)与g(x)=(
)x的图象关于直线y=x对称，则f(4—x2)的单调递增区间是 （ ）
A．
B．
C．
D．
11．已知
，则
的大小关系是 （ ）
A．
B． 
C． 
D． 
12．据2002年3月5日九届人大五次会议《政府工作报告》：“2001年国内生产总值达到95933亿元，比上年增长7.3%．”如果“十·五”期间(2001年—2005年)每年的国内生产总值都按此年增长率增长，那么到“十·五”末我国国内年生产总值约为 （ ）
A．115,000亿元 B．120,000亿元 C．127,000亿元 D．135,000亿元
二、填空题：(本大题共4个小题，每小题4分，共16分)
13．设集合A={xx＜4＝，B={xx2－4x＋3＞0}， 则集合{xx∈A且
= ．
14．函数y=－(x－1)2(x≤0)的反函数为 ____．
15．已知集合M={x
＋x≤(
)x－2，x∈R}，则函数y=2x的值域是___
_______．
16．周长为l的铁丝弯成下部为矩形，上部为半圆形的框架(半径为r)，若矩形底边长为2x，此框架围成的面积为y，则y与x的函数解析式是 .
三、解答题：(本大题共6个小题， 共74分)
17．(本小题满分12分)
求下列函数
的定义域、值域和单调区间．
18．(本小题满分12分)
已知集合
19．(本小题满分12分)
已知f(x)=
，且点M(2，7)是y=f－1(x)的图象上一点．
（1）求f(x)和f－1(x)的解析式；
（2）求y=f－1(x)的值域；
（3）求y=f(x)的值域，并作y=f(x)的图象．
20．(本小题满分12分)
已知集合M是满足下列性质的函数f(x)的全体：存在非零常数T，对任意x∈R，
有f(x＋T)=T f(x)成立．
（1）函数f(x)= x 是否属于集合M？说明理由；
（2）设函数f(x)=ax(a＞0，且a≠1)的图象与y=x的图象有公共点，证明：f(x)=ax∈M。
21．(本小题满分13分)
已知函数f(x)=
，x∈[1，＋∞
（1）当a=时利用函数单调性的定义判断其单调性，并求其值域．
（2）若对任意x∈[1，＋∞，f(x)＞0 恒成立，求实数a的取值范围．
22．(本小题满分13分)
某厂生产某种零件，每个零件的成本为40元，出厂单价定为60元． 该厂为鼓励销售商订购，决定当一次订购量超过100个时，每多订购一个，订购的全部零件的出厂单价就降低0.02元，但实际出厂单价不能低于51元．
（1）当一次订购量为多少个时，零件的实际出厂单价恰降为51元？
（2）设一次订购量为x个，零件的实际出厂单价为P元，写出函数
的表达式；
（3）当销售商一次订购500个零件时，该厂获得的利润是多少元？如果订购1000个，
利润又是多少元？(工厂售出一个零件的利润=实际出厂单价－成本)
参考答案
一、选择题： CDDCA ADCAC BC
二、填空题：13. [1，3]． 14.
≤－1)．
15.［
，2］． 16.y=－(π+2)x2+lx+
r2(0＜x＜
).
三、解答题：
17.解析：①原函数的定义域是
；
②由，得
，
，∴
，∴
，∴原函数的值域是
；
③∵
，
又当
，
从而
；
当
，
从而
．
18.解析: 
①
时，
满足
;
②
时，
， ∵ ， ∴
③
时，
， ∵
∴
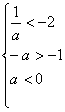
综合①②③可知:
的取值范围是:
19.解析：(1)由已知条件可知，点(7，2)在函数y=f(x)的图象上，
∴f(7)=2，即
=2，解得a=
∴f(x)=
，f－1(x)=
(2)要使函数f(x)有意义，必须且只须7x－7≠0，即x≠1，
∴函数f(x)的定义域为{x∈Rx≠1}
即y=f－1(x)的值域为(－∞，1)∪(1，＋∞)
(3) 要使函数f－1(x)有意义，必须且只须7x－9≠0，即x≠
，
∴函数f－1(x)的定义域为{x∈Rx≠}
即y=f(x)的值域为{x∈Rx≠}
(或直接求：f(x)= =
×
)
20.解析：(1)对于非零常数T，f(x＋T)=x＋T， Tf(x)=Tx．
因为对任意x∈R，x＋T= Tx不能恒成立，所以f(x)=
(2)因为函数f(x)=ax(a＞0且a≠1)的图象与函数y=x的图象有公共点，
所以方程组：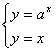
有解，消去y得ax=x，
显然x=0不是方程ax=x的解，所以存在非零常数T，使aT=T．
于是对于f(x)=ax有
故f(x)=ax∈M．
21.解析：(1)f(x)=x＋
，任取x1，x2∈[1，＋∞且x1＜x2
f(x1)－f(x2)=x1＋
－x2－
=(x1－x2)(1－
)
当a=时，f(x1)－f(x2)=(x1－x2)(1
)
∵1≤x1＜x2，∴x1－x2＜0，
1＞0
∴f(x1)－f(x2)＜0，即f(x1)＜f(x2)，∴f(x)是增函数
当x=1时，f(x)取得最小值为f(1)=1＋
∴值域为
(2)f(x)=
．
设g(x)=x2＋2x＋a，x∈[1，＋∞
∵g(x)的对称轴为x=－1 ∴只需g(1)＞0 便可，g(1)=3＋a＞0，∴a＞－3
另解：g(x)＞0得a＞－x2－2x=－(x＋1)2＋1
∵x∈[1，＋∞，∴当x=1时，－x2－2x取得最大值为－3．
∴a﹥3
22.解析：(1)设每个零件的实际出厂价恰好降为51元时，一次订购量为
个，则
因此，当一次订购量为550个时，每个零件的实际出厂价恰好降为51元．
(2)当
时，P=60；
当
时，
；
当
所以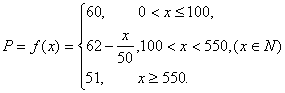
(3)设销售商的一次订购量为
个时，工厂获得的利润为L元，则
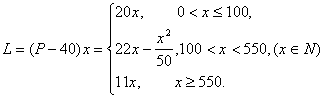
当x=500时，L=6000；当x=1000时，L=11000．
因此，当销售商一次订购500个零件时，该厂获得的利润是6000元；
如果订购1000个，利润是11000元．