第一学期高一期中考试
数 学 试 卷
本试卷分第I卷（选择题）和第II卷（非选择题）两部分。共150分，考试时间120分钟。
第I卷（选择题 共60分）
一、选择题（本小题12个小题，每小题5分，共60分，在每小题列出的四个选项中，只有一项是符合题目要求的。）
1．设全集U={0，1，2，3，4}，集合A={0，1，2，3，}，B={2，3，4}，则（
uA）∪（uB）
= （ ）
A．{0} B．{0，1} C．{0，1，4} D．{0，1，2，3，4}
2．设f(x)=2x+3,g(x+2)=f(x),则g(x)等于 （ ）
A．2x+1 B．2x－1 C．2x－3 D．2x+7
3．函数y=2－
的值域是 （ ）
A．[－2，2] B．[1，2] C．[0，2] D．[－
，]
4．如果函数f(x)=x2+2(a－1)x+2在区间（－∞，4
上是减函数，那么实数a的取值范围是（ ）
A．a≥ －3 B．a≤－3 C．a≤5 D．a≥ 3
5．若函数f(x)的图象过（0，－1）点，则函数f(x+4)的反函数的图象必经过 （ ）
A．（1，－4） B．（－4，－1） C．（4，－1） D．（－1，－4）
6．已知函数y=4x－3·2x+3,当其值域为[1，7]时，x的取值范围是 （ ）
A．[2，4] B．
C．（0，1）∪[2，4）D．∪[1，2]
7．若0<a<1,b<－1，则函数f(x)=ax+b的图象不经过 （ ）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
8．下列命题
①“等边三角形的三内角均为60°”的逆命题
②若k>0，则方程x2+2x－k=0有实根“的逆命题
③“全等三角形的面积相等”的否命题
④“若ab≠0，则a≠0”的逆否命题，其中真命题的个数是 （ ）
A．0个 B．1个 C．2个 D．3个
9．若x2－3x+2≠0是x≠1的 （ ）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
10．给定两个命题p、q，则可组成四个复合命题“┐p”、“┐q”、“p或q”、“p且q”,这四个复合命题中，真命题的个数为a，假命题的个数为b，则a、b的大小关系是 （ ）
A．a>b B．a<b C．a=b D．以上都不对
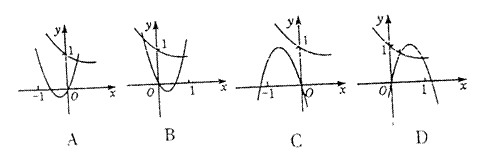11．在下列图象中，二次函数y=ax2+bx与指数函数y=（
）x的图象只可能是 （ ）
12．函数f(x)=
的定义域为R，则k的取值范围是 （ ）
A．0≤k<
B．0<k< C．k<0或k> D．0<k≤
第Ⅱ卷（非选择题 共90分）
二、填空题（本大题共4小题，每小题4分，共16分，把答案填在题中横线上）
13．化简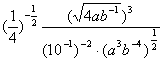
的结果是 .
14．已知函数f(x)=ax+a－x(a>0,a≠1)， 且f(1)=3, 则, f(0)+f(1)+f(2)的值是 .
15．函数f(x)=
的定义域为
.
16．方程3x2－10x+k=0(k∈R)有相异的两个同号实根的充要条件是 .
三、解答题（本大题共6小题，共74分，解答应写出文字说明、证明过程或演算过程）
17．（本小题满分12分）
已知命题p：不等式x－1>m－1的解集为R，命题q：f(x)=－(5－2m)x是减函数，若p或q为真命题，p且q为假命题，求实数m的取值范围.
18．（本小题满分12分）
定义符号函数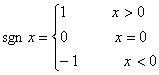
解不等式：x+2>(2x－1)sgnx
19．（本小题满分12分）
已知函数f(x)=ax(a>0,a≠1)
（I）若f(x)在[1，2]中最大值比最小值大
，求a的值；
（Ⅱ）若f(x)在[－2，2]上的函数值总小于2，试求a的取值范围.
20．（本小题满分12分）
设点M（－1，－2）既在函数y=ax2+b(x≤0)的图象上，又在其反函数的图象上.
①求反函数f－1(x).
②证明反函数在其定义域内的单调性.
21．（本小题满分12分）
已知函数f(x)=px2－2x+q(p≠0，0≤x≤1)的最小值为 1.
（I）求以p表示q的解析式q=f(p)；
（Ⅱ）作出函数q=f(p)的图象.
22．（本小题满分14分）
用水清洗一堆蔬菜上残留的农药，对用一定量的水清洗一次的效果作如下假定：用1个单位量的水可洗掉蔬菜上残留农药量的
，用水越多洗掉的农药量也越多，便总还有农药残留在蔬菜上.设用x的单位量的水清洗一次以后，蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数f(x).
（1）试规定f(0)的值，并解释其实际意义；
（2）试根据假定写出函数f(x)应该满足的条件和具有性质；
（3）设f(x)= 
,现在a(a>0)单位量的水，可以清洗一次，也可以把水平均分成2份后清洗两次，试问用哪种方案清洗后蔬菜上残留的农药量比较少？说明理由.
高一数学试题参考答案
一、选择题：
1．C 2．B 3．C 4．B 5．D 6．D 7．A 8．C 9．A 10．C 11．C 12．A
二、填空题：
13．
14．12 15．[－2，1] 16．0<k<
三、解答题：
17．解：不等式x－1<m－1的解集为R，须m－1<0
即p是真 命题，m<1……………………（4分）
f(x)=－(5－2m)x是减函数，须5－2m>1即q是真命题，m<2…………（8分）
由于p或q为真命题，p且q为假命题
故p、q中一个真，另一个为假命题 因此，1≤m<2…………（12分）
18．解：不等式可分如下情况
（1）
解之得0<x<3……………………（3分）
（2）
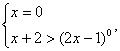解之得x=0……………………（6分）
（3）
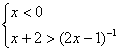，解之得－
<x<0…………（10分）
综上述，不等式的解集为（－，3）………………（12分）
19．解：（I）因为指数函数y=ax是单调函数……………………（1分）
所以有a2－a=…………（3分） 解得
…………（5分）
（II）由于ax<2, 对于任意x∈[－2，2]成立，
因此，y= ax(－2≤x≤2)的最大值小于2…………………………7分
（1）当0<a<0时，a－2<2即可解得
<a<0……………………9分
（2）当a>1时，a2<2即可解得1<a<…………………………11分
故a的取值范围是
………………………………12分
20．解：（1）由点M（－1，－2）既在函数y=ax2+b(x≤0)的图象上，又在其反函数的图象上，故M′（－2，－1）在y=ax2+b(x≤0)的图象上，有：………………（2分）
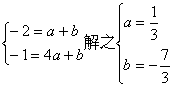…………………………………………4分
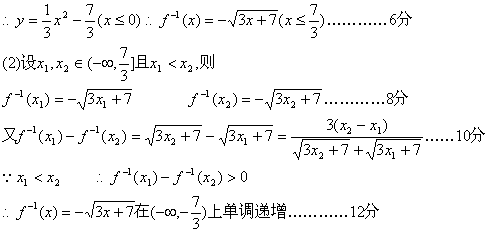
21．解：（I）f(x)=p(x－
)2+q－(p≠0,0≤x≤1).…………………………（2分）
当<0,即p<0时，f(x)在[0，1]上是减函数
此时f(x)最小值=f(1)=p+q－2=1,故q=3－p. ……………………4分
当p>0且≤1，即p≥1时，f(x)最小值f()=q－=1,故q=1+
.…………（6分）
|
>1，即0<p<1时，f(x)最小值=f(1)=p+q－2=1故q=3－p……（8分）
于是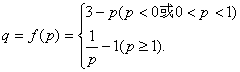
………………（9分）
（II）函数图象见图，（酌情赋分）………………12分
22．解（1）f(0)=1表示没有用水洗时，蔬菜上的农药量将保持原样，…………2分
（2）函数f(x)应该满足的条件和具有的性质是：f(0)=1,f(1)=,
在[0，+∞）上f(x)单调递减，且0<f(x)≤1.……………………（6分）
（3）设仅清洗一次，残留的农药量为
，清洗两后，残留的农药量为
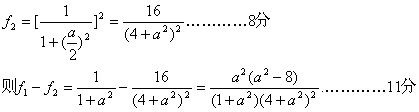
于是，当a>2时，f1>f2 ；当a=2时，f1=f2 ；当0<a<2时，f1<f2.……（13分）
因此，a>2时，清洗两次后残留的农药量较少；
当a=2时，两种清洗方法具有相同的效果；
当0<a<2时，一次清洗残留的农药量较少……………………（14分）