不等式
一．选择题
1．若a<b<c,下列结论正确的是（ ）
A．c·
>b·
B．bc≥ac C．b-c>a-c D．
2．以下四个条件中，能使
成立的充分条件的个数是（ ）
①b>0>a ②0>a>b ③a>0>b ④a>b>0
A．1个 B．2个 C．3个 D．4个
3．若
且
1，
，
，则M、N之间的大小关系是（ ）
A．M>N B．M<N C．M=N D．M、N大小关系不定
4．设a,b是满足ab＜0的实数，则（ ）
A．∣a+b∣＜∣a-b∣ B．∣a+b∣＞∣a-b∣
C．∣a-b∣＜∣a∣-∣b∣ D．∣a-b∣＜∣a∣+∣b∣
5．已知a＞b＞c，则
的值（ ）
A．正数 B．负数或零 C．非负数 D．不确定
6．不等式ax2+bx+c>0的解是0<α<x<β,则不等式cx2－bx+a>0的解集是（ ）
A．
B．
C．
D．
7．不等式
（ ）
A．{x-3<x<-2} B．{x-2<x<0} C．{x0<x<2} D．{xx<-3或x>2}
8．f(x)=3ax+1-2a,在[-1，1]上存在x0，使f(x0)=0(x0≠±1)，则a的取值范围是（ ）
A．-1<a<
B．a> C．a>或a<-1 D．a<-1
9．不等式
的解集是（ ）
A．（-2，0） B．（-2，-1）
C．（-2，-1）∪（
，1）
D．（-1,-）∪(,1)
10．不等式
的解是（ ）
A．
B．
C．
Ｄ．
11．下列函数中，最小值为4的函数为（ ）
A．
B．
C．
D．
12．已知方程x2+(m+2)x+m+5=0有两个正根，则实数m的取值范围是（ ）
A．m<-2 B．m≤-4 C．m>-5 D．-5<m≤-4
13．已知函数f（x）＝︱lgx︱，若
，则（ ）
A．f(a)>f(b)>f(c) B．f(b)>f(a)>f(c) C．f(c)>f(b)>f(a) D．f(c)>f(a)>f(b)
14．已知二次函数f（x）=x2+x+a（a>0）,若f（m）＜0，则f（m+1）的值为（ ）
A．正数 B．负数 C．零 D．符号与a有关
15．某电脑用户计划用不超过500元的资金购买单价分别为60元、70元的单片软件和盒装磁盘．根据需要，软件至少买3片，磁盘至少买2盒，则不同的选购方式共有（ ）
A．5种 B．6种 C．7种 D．8种
16．已知实数
、
满足
，则代数式
的值（ ）
A．有最小值但没有最大值 B．有最大值但没有最小值
C．既有最大值也有最小值 D．没有最大值也没有最小值
17．若不等式
在
内恒成立，则实数
的取值范围是（ ）
A．
B．
C．
D．
18．已知
，且
，则使不等式
恒成立的
的最小正整数值是（ ）
A．2 B．3 C．4 D．5
19．一批救灾物资随26辆汽车从某市以V公里/小时速度匀速直达灾区，已知两地路程400公里，为了安全起见，两辆汽车的间距不得小于
公里，那么这批物资全部到达灾区，最少需要（ ）
A．5小时 B．10小时 C．15小时 D．20小时
20．若
，
，则
的取值范围是（ ）
A．
B．
C．
D．
二．填空题
21．设a>b>0,m>0,n>0,则p=
,q=
,r=
,s=
的大小顺序是
．
22．设条件甲“1＜
且0＜
”，乙“0＜
＜1且1＜
＜3”，那么甲
大是乙成立的 条件．
23．若
的最大值是
．
24．若关于x的实系数二次方程x2+px+8=0有不等实根α和β，则必有①
②
， ③
，
④
，
上述结论中，正确结论的序号是 ．
25．不等式
的解集是 ．
26．若a>0,使关于x的不等式
在R上的解集不是空集，则a的取值范围是
．
27．当x=3时，不等式
成立，则此不等式中x的解集是
．
28．建造一个容积为8m3，深为2m的长方体无盖水池，如果池底和池壁的造价每平
方米分别为120元和80元，那么水池的最低总造价为 元．
29．设数列{an}的通项公式an=
，则an中的最大项是第
项．
30．
，且
，则
的最小值为
．
三．解答题
31．已知x、y是非零实数，试比较
的大小．
32．(1)已知a,b,c
R,且a+b+c=1,求证a2+b2+c2＞
;
(2)已知a,b,c为不等正数，且abc=1,求证
33．已知a，b，c均为正数，求证：
．
34．设f(x)=
,a,b满足f(a)=f(b)=2f(
)的实数，其中0＜a＜b．
(1)求证：a＜1＜b
(2)求证：2＜4b-b2＜3．
35．是否存在满足下列条件的二次函数f(x)：
（1）当
； （2）
．
若存在，求出其解析式；若不存在，说明理由．
36．解下列不等式：（1）
； （2）
．
37．已知
，
（1）求f(x)的表达式； （2）若f(x)为奇函数，求t的值；
（3）若f(x)是奇函数，解关于x的不等式
．
38．解不等式：
．
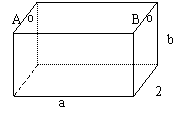39．如图为处理含有某种杂质的污水，要制造一底宽为2米的无盖长方形沉淀 箱，污水从A孔流入，经沉淀后从B孔流出，设箱体的长度为a米，高为b米，已知流出的水中该杂质的质量分数与a，b的乘积ab
成反比，现有制箱材料60平方米，问当a，b各为
多少时，经沉淀后流出的水中该杂质的质量分数最
小？（A、B孔的面积忽略不计）
40．设
为
的根，且
，令
．
(1)证明：
； (2)证明：
；
(3)证明：
．