第一学期期中考试高一数学试卷
第I卷（选择题 共60分）
一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。
1、已知点P（-4m,3m），（m﹥0）那么2sin
+cas的值是
（ ）
A、
B、±
C、－
D、与m值有关
2、tan300°+cot405°的值是 （ ）
A、1+
B、1－ C、-1－ D、-1+
3、设
是第二象限角，
cos
=- cos,则是
（ ）
A、第一象限角 B、第二象限角 C、第三象限角 D、第四象限角
4、若sin=
,tan(
)=1,且是第二象限角，则tan
的值是 （ ）
A、
B、- C、7
D、-7
5、若函数
=3sin(
)对一切
R都有f (
+χ)=f (-χ)，则f()
等于 （ ）
A、0 B、3 C、-3 D、3或-3
6、设=asin(
x+)+bcos(x+),其中a、b、、均为非零实数，若f(2003)=-1,则f(2005)等于
（ ）
A、-1 B、0 C、1 D、2
7、函数=cos(sinX)的最小正周期T及最小值m分别为
（ ）
A、T=，m=1 B、T=
，m=cos1 C、T=，m=cos1 D、T=2,m=-1
8、函数y=sin2χ+2cosχ,(≤χ≤
)的最小值为
（ ）
A、-2 B、-
C、1
D、
9、已知=sin(
+
)+cos(+)为奇函数，则
的一个取值可为 （ ）
A、0
B、-
C、 D、
10、在
ABC中， tanA ·
tanB﹤1,则这个三角形是
（ ）
A、锐角三角形 B、钝角三角形 C、直角三角形 D、以上都有可能
11、要得到y=-sin(－2χ)图像，只需将y=sin2χ的图像
（ ）
A、向左平移
B、向右平移 C、向左平移 D、向右平移
12、若函数=Asin(2χ+
)cos(2χ+)+a在区间[0，]上的图象被直线y =2 和y=0的截得的弦长相等（不为0），则必有
（ ）
A、A＞2，a=1 B、A≤2，a=0 C、 A＞2，a=0 D、A≤2，a=1
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
第Ⅱ卷（非选择题 共90分）
二、填空题：本大题共4小题，每小题4分，共16分。把答案填在横线上。
13、设扇形的周长为8㎝，面积为4㎝2，则扇形的圆心角的弧度数是
14、设χ是不等边三角形的最小角，且cosχ=a－
,则实数a的取值范围是
15、已知在ABC中，3sinA+4cosB=6，4sinB+3cosA=1,则角C的大小为
16、给出下列四个命题：
①函数y=-sin(k+χ)( k∈z)是奇函数。
②函数y=(sinχ＋cosχ)2＋cos2χ的最大值为3。
③函数y=sin(2χ+)的图象关于直线χ=-
对称。
其中正确命题的序号是 。
三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或推演步骤。
17、设是第二象限角，sin=
,求sin(
-2)的值。
18、化简：cos2＋cos2(＋60°)－cos·cos(＋60°)
19、化简求值：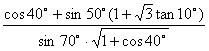 
20、证明：
=
21、已知函数=Asin
(其中A、B、
是实常数且＞0)的最小正周期为2，并且当
=
时，的最小值为2。
（1）求函数的解析式；
（2）函数y=（∈R）的图象是否在闭区间[
，
]上存在对称轴？若存在，求出其对称轴方程，若不存在，请说明理由。
22、已知函数=log
（1）求的定义域和值域；
（2）判断的奇偶性，并求的周期；
（3）指出的单调区间。