典例剖析(第二章 函数)
[例1]如图2-30,某房地产开发公司要在荒地ABCDE上划分一块长方形地面(不改变方位)建造一幢公寓.问如何设计才能使公寓占地面积最大?并求出最大面积(精确到1m2).
【解】 设公寓占地矩形的长和宽分别为a、b,面积为S
![]() (70≤a≤100,60≤b≤80)
(70≤a≤100,60≤b≤80)
∴b=![]() ,且70≤a≤100
,且70≤a≤100
S=a·b=![]()
=![]()
当a=95∈[70,100]时,S取到最大值约为6017 m2.
【点评】
本问题即已知b=![]() ,70≤a≤100,60≤b≤80,求S=a·b的最大值,可通过代入消元转化为关于a的二次函数问题,在此过程中,特别要注意函数的定义域即变量a的取值范围.
,70≤a≤100,60≤b≤80,求S=a·b的最大值,可通过代入消元转化为关于a的二次函数问题,在此过程中,特别要注意函数的定义域即变量a的取值范围.
[例2]已知f(x)=x2+c,且f[f(x)]=f(x2+1),
(1)设g(x)=f[f(x)],求g(x)的解析式;
(2)设φ(x)=g(x)-λf(x),试问是否存在实数λ,使φ(x)在(-∞,-1)内是减函数,并在(-1,0)内是增函数.
【解】 (1)由f[f(x)]=f(x2+1)即(x2+c)2+c=(x2+1)2+c
整理得(c-1)(2x2+c+1)=0,∴c=1
∴g(x)=x4+2x2+2
(2)φ(x)=g(x)-λf(x)=(x4+2x2+2)-λ(x2+1)=x4+(2-λ)x2+2-λ
设y=φ(x),x2=t
则y=t2+(2-λ)t+2-λ在(0,1)上递减,且在(1,+∞)上递增
∴-![]() =1,即λ=4
=1,即λ=4
【点评】 本题主要利用了数学中最基本的思想方法:待定系数法和换元法,转化为二次函数的单调性问题.
[例3]已知函数f(x2-3)=lg![]() ,
,
(1)求f(x)的定义域;
(2)求f(x)的反函数f-1(x).
【解】 (1)设t=x2-3,则x2=t+3,且t>-3 ①
f(t)=lg![]() ,
,
又![]() >0,∴t<-3或t>3 ②
>0,∴t<-3或t>3 ②
因此由①,②知,f(x)=lg![]() 的定义域为(3,+∞)
的定义域为(3,+∞)
(2)设y=lgu,u=![]() ,x>3
,x>3
则u>1,∴y=lgu>0
由y=lg![]() 得10y=
得10y=![]()
∴x=![]()
f(x)的反函数f-1(x)= ![]() (x>0)
(x>0)
【点评】
本题使用换元法求出函数f(x)的解析式及其定义域.但要注意求f(t)的定义域的条件:其一,先由f(x2-3)=lg![]() 有意义得到
有意义得到![]() >0,即x2>6,再由t=x2-3>3,即t>3;其二,换元后f(t)=lg
>0,即x2>6,再由t=x2-3>3,即t>3;其二,换元后f(t)=lg![]() 有意义得到
有意义得到![]() >0,即t<-3或t>3.然后取二者交集得定义域,而求其反函数时,要注明反函数定义域,即要求出原函数值域.
>0,即t<-3或t>3.然后取二者交集得定义域,而求其反函数时,要注明反函数定义域,即要求出原函数值域.
[例4]已知二次函数f(x)=ax2+bx满足f(2)=0且方程f(x)=0有等根.
(1)求f(x)的解析式;
(2)问是否存在实数m,n(m<n),使f(x)的定义域为[m,n],值域为[2m,2n],如存在,求出m,n的值,如不存在,说明理由.
【解】 (1)依题意,方程ax2+(b-1)x=0有等根
∴(b-1)2=0即b=1
又f(2)=0,
∴4a+2b=0,∴a=-![]()
∴f(x)=-![]() x2+x
x2+x
(2)∵f(x)=-![]() (x-1)2+
(x-1)2+![]() ≤
≤![]()
∴2n≤![]() ,即n≤
,即n≤![]()
∵f(x)=-![]() (x-1)2+
(x-1)2+![]() 的对称轴为x=1
的对称轴为x=1
∴当n≤![]() 时,f(x)在[m,n]上为增函数.
时,f(x)在[m,n]上为增函数.
设m,n存在,则![]()
即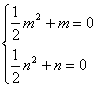
又m<n≤![]() ,∴
,∴![]()
即存在实数m=-2,n=0,使f(x)的定义域为[-2,0],值域为[-4,0].
【点评】 二次函数问题是函数中的重要题型,本题先用待定系数法确定解析式,然后再用m,n把定义域、值域联系起来,考查二次函数性质.
[例5]已知f(x)在R上是增函数,且f(k·3x)-f(9x-3x+2)<0对任意的x∈R都成立,求实数k的取值范围.
【解】 由已知f(k·3x)<f(9x-3x+2)对x∈R恒成立.
∵f(x)在R上是增函数
∴只要k·3x<9x-3x+2对x∈R恒成立.
【法一】 令t=3x,则t>0,上式等价于g(t)=t2-(k+1)t+2>0
对t∈(0,+∞)恒成立.
根据二次函数的图象性质得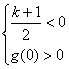 或
或
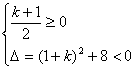
即![]() 或
或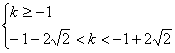
∴k<2![]() -1
-1
【法二】
分离常数k得k<3x+![]() -1对一切x∈R恒成立.
-1对一切x∈R恒成立.
令h(x)=3x+![]() -1只要k<h(x)的最小值.
-1只要k<h(x)的最小值.
∵h(x)=3x+![]() -1≥2
-1≥2![]() -1=2
-1=2![]() -1
-1
∴h(x)的最小值为2![]() -1
-1
∴k<2![]() -1.
-1.
故所求k的取值范围是(-∞,2![]() -1).
-1).
【点评】 对于没有给出具体解析式的抽象函数f(x),如果知其单调性,就可以脱去函数值不等式中的函数符号,本题还充分说明了二次函数图象和性质的工具性作用,对于不等式恒成立问题,分离常数并构造函数求出其最值来确定常数取值范围不失为一个简单有效的方法.