对数函数

高中45分钟过关检测

§2.8　对数函数

一、选择题(每小题3分，共15分)

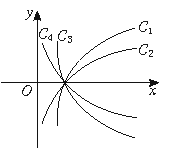
1.图中曲线是对数函数y=log_ax的图象，已知a取四个值，则相应于C₁，C₂，C₃，C₄的a值依次为

A.　　　　　　　　　　　　　　　　　　　　　　　 B.

C.　　　　　　　　　　　　　　　　　　　　　　　 D.

2.函数y=的定义域为

A.(,+∞)　　　　　　　　　　　　　　　　　　　　　　　　　　　B.［1,+∞

C.( ,1　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.(－∞,1］

3.函数y=lg(－1)的图象关于

A.x轴对称　　　　　　　　　　　　　　　　　　　　　　　　　　　B.y轴对称

C.原点对称　　　　　　　　　　　　　　　　　　　　　　　　　　 D.直线y=x对称

4.已知，则a、b的关系是

A.1＜b＜a　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.1＜a＜b

C.0＜a＜b＜1　　　　　　　　　　　　　　　　　　　　　　　　　　　　D.0＜b＜a＜1

5.已知A={x2≤x≤π}，定义在A上的函数y=log_ax(a＞0且a≠1)的最大值比最小值大1，则底数a的值为

A.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.

C.π－2　　　　　　　　　　　　　　　　　　　　　　　　　　　　　D. 或

二、填空题(每小题3分，共15分)

6.设函数f(x)=在区间(－，0)上恒有f(x)>0,则a的取值范围是__________.

7.函数y=(0.2)^x－1的反函数是__________.

8.已知log_a<1,则a的取值范围是__________.

9.函数f(x)=lgx，则f(),f(),f(2)的大小关系是__________.

10.函数f(x)=x²－2ax+a+2，若f(x)在［1，+∞)上为增函数，则a的取值范围是__________，若f(x)在［0，a］上取得最大值3，最小值2，则a=__________.

三、解答题(共20分)

11.(6分)已知m>1,试比较(lgm)^0.9与(lgm)^0.8的大小.

12.(7分)已知f(x)=(3－2x－x²)，求y=f(lgx)的定义域、值域、单调区间.

13.(7分)已知函数f(x)=log_a(a－a^x)且a>1，

(1)求函数的定义域和值域；

(2)讨论f(x)在其定义域上的单调性；

(3)证明函数图象关于y=x对称.

参考答案

一、1.A  2.C　3.C　4.D  5.D

二、6.－＜a＜－1或1＜a＜

7.y=log_0.2(x+1)(x＞－1)

8.a＞1或0＜a＜

9.f()＞f()＞f(2)

10.(－∞,1］　1

三、11.解：当lgm＞1即m＞10时，(lgm)^0.9＞(lgm)^0.8；

当lgm=1即m=10时，(lgm)^0.9=(lgm)^0.8；

当0＜lgm＜1即1＜m＜10时,(lgm)^0.9＜(lgm)^0.8.

12.定义域［，10］，值域［0，2］，增区间［，］，减区间［，10］

13.(1)定义域为(－∞,1)，值域为(－∞,1)

(2)解：设1＞x₂＞x₁

∵a＞1,∴，于是a－＜a－

则log_a(a－a)＜log_a(a－)

即f(x₂)＜f(x₁)

∴f(x)在定义域(－∞,1)上是减函数

(3)证明：令y=log_a(a－a^x)(x＜1)

则a－a^x=a^y,x=log_a(a－a^y)

∴f^－1(x)=log_a(a－a^x)(x＜1)

故f(x)的反函数是其自身，得函数f(x)=log_a(a－a^x)(x＜1)

图象关于y=x对称.