高一第二学期数学期中考试试卷（七）
一、选择题：（5’×12=60’）
1、在直角坐标系中，若角
线，则：( )
A、
B、
C、
D、
2、函数y=
在闭区间：
( )
A、
上是增函数
B、
上是增函数
C、
上是增函数
D、
上是增函数
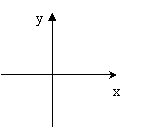
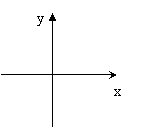
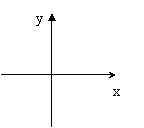
3、函数y=
的大致图象是：
( )
 |  |  |  |
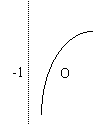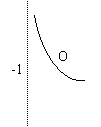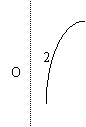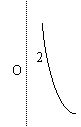A B C D
4、已知f(x)=
，则f(x)是：
( )
A、周期为3
的偶函数
B、周期为3的奇函数
C、周期为2的偶函数
D、周期为2的奇函数
5、函数y=sinx+cosx（0<x<
的值域为：
( )
A、（0，
B、（1，
C、 [1， D、[-
6、所对弦长等于其所在圆半径的
倍的圆心角（正角）的弧度数是：( )
A、2
B、
C、
D、
7、两向量共线是两向量相等的： ( )
A、充分但不必要条件 B、必要但不充分条件
C、充要条件 D、既不充分也不必要
8、要得到函数y=
的图象，只要将函数y=sin2x的图象： ( )
A、向左平移
B、向右平移
C、向左平移
D、向右平移
9、已知数列{an}满足an=-2n+25，则使Sn达到最大值时，n为 ( )
A、13 B、12 C、11 D、10
10、函数f(x)=sin(2x+
)图象的一条对称轴方程是
，则的值是：
A、
B、
C、
D、
( )
11、
，
，则
的值： ( )
A、
B、
C、
D、
12、已知：偶函数y=f(x)在[-1，0]上为单调递减函数，又
、
为锐角三角形的两内角，则：
( )
A、
B、
C、
D、
二、填空题：（4’×4=16’）
13、化简：
_____________________
14、函数
的定义域_________________________
15、
按从小到大排列，其顺序是__________。
16、设角A是
中的最小角，且cosA=
，则实数a的取值范围____________。
三、解答题
17、化简求值
（1）
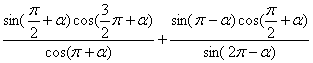（4’）
（2）
)
(6’)
18、已知：、为锐角，
，
，求cos (12’)
19、若方程
的两根
的比是3:2，求p、q的值。（12’）
20、某公司由于新开发的产品科技含量高，因而预计第一年产量的增长率是200%，根据市场预测，以后每年产量的增长率应是前一年增长率的一半。（1）4年后，产品的预计产量是原来的多少倍？（2）由于生产过程中的损耗，每年产品的实际产量比预计的少5%，那么经过多少年后公司的产品实际产量开始下降？（12’）
21、设函数
的最小值为g(a)
(1)求g(a)的表达式 （2）若g(a)=
，求此时f(x)的最大值 （14’）
22、已知：、
，角、满足条件：
（1）证明：
（2）求
的值域 （14’）
参考答案
一．选择题 （12×5’=60’）
DDDAB，DBDBA，CA
二．填空题 （4×4’=16’）
13．-9
+9
；
14. {x 2kp+<x<2kp+
, kÎZ }
15. cos
<sin
<tan(
); 16. a≥3
三．解答题(17题 10’，18、19，20题 12’21、22题 14’)
17.
(1) 原式=
+
=0-----------------------------------
-
(2)sin
(tan
－)= sin
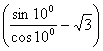
= sin
--------------------------------------------
= sin
--------------------------------------------------
=
------------------------------------------------------
=－1
---------------------------------------------------
18.解：, 
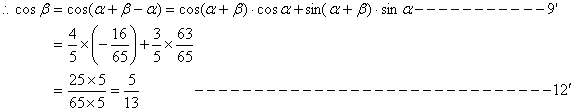19.解 
展开
并整理得：2tan²q+5tanq－3=0
(1)------------------------------3’
∴tanq = 或tanq =－3------------------------------------------------------------------5’
根据一元二次方程韦达定理得.
------------------------------------------------------8’
20.解：设公司原来的产量为a，n年后产品的预计产量为an，
则有a1=a（1+2）
a2=3a（1+
）=6a
a3=6a（1+）=9a
a4=9a（1+
）=
a
∴4年后，预计产量是原来的倍。---------------------------------------5’
(2)设n年后的实际产量为an
∴an＋1= an（1+
---------------------------------------------------7’
依题意：an≥an（1+-------------------------------------------8’
∴1+
≤
∴
≥19 -----------------------------------------------------------------------10’
∴n≥6------------------------------------------------------------------------------11’
∴6年后产品的实际产量开始下降。---------------------------------------12’
21．解：（1）f（x）=2cos2x－2acosx－2a－1
=2（cosx
-------------------------------1’
∵－1≤cosx≤1
∴①当
≥1即a≥2时，cosx=1，g（a）=1—4a ------------------3’
②当—2<a<2时,cosx=时,g(a)=－
－２a－１
------------------5’
③当a≤－2时,cosx=－1时,g(a) = 1 -----------------7’
∴
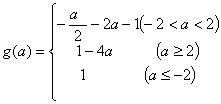----------------------------------8’
(2)若g(a)= =1－4a,则a=
---------------------------10’
∴只有－－２a－１=, ∴a=－１或a=－３-------------------11’
∴a=－３Ï（－２，２） ∴a=－１适合-------------------------12’
当a=－１时, f(x)=2（cosx
∴当cosx=1时, f(x)max = 5 -------------------------------14’
22.解: (1)sinβ=sinαcosαcosβ－sin2αsinβ
∴sinβ(1+ sin2α)= sinαcosαcosβ----------------------------------2’
∴cosβ≠0
∴tanβ=
----------------------------------------------------4’
=
--------------------------------------------6’
=
----------------------------------------------------7’
（2）令x=tanα （x > 0）
则tanβ=y=
∴2yx2－ｘ+y=0--------------------------------------------------------9’
必须D=1－8 y2 ≥0且y>0------------------------------------------12’
∴0<y≤
----------------------------------------------14’