高中数学苏教版必修4
三角函数 三角恒等变换知识点总结
一、角的概念和弧度制：
（1）在直角坐标系内讨论角：
角的顶点在原点，始边在
轴的正半轴上，角的终边在第几象限，就说过角是第几象限的角。若角的终边在坐标轴上，就说这个角不属于任何象限，它叫象限界角。
（2）①与
角终边相同的角的集合：
与角终边在同一条直线上的角的集合： ；
与角终边关于轴对称的角的集合：
；
与角终边关于
轴对称的角的集合：
；
与角终边关于
轴对称的角的集合：
；
②一些特殊角集合的表示：
终边在坐标轴上角的集合： ；
终边在一、三象限的平分线上角的集合： ；
终边在二、四象限的平分线上角的集合： ；
终边在四个象限的平分线上角的集合： ；
（3）区间角的表示：
①象限角：第一象限角： ；第三象限角： ；
第一、三象限角： ；
②写出图中所表示的区间角：
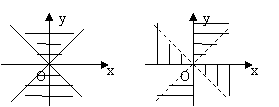
（4）正确理解角：
要正确理解“
间的角”=
；
“第一象限的角”= ；“锐角”= ；
“小于
的角”=
；
（5）由的终边所在的象限，通过
来判断
所在的象限。
来判断
所在的象限
（6）弧度制：正角的弧度数为正数，负角的弧度数为负数，零角的弧度数为零；任一
已知角的弧度数的绝对值
，其中
为以角作为圆心角时所对圆弧的长，
为圆的半径。注意钟表指针所转过的角是负角。
（7）弧长公式： ；半径公式： ；
扇形面积公式： ；
二、任意角的三角函数：
（1）任意角的三角函数定义：
以角
的顶点为坐标原点，始边为轴正半轴建立直角坐标系，在角的终边上任取一个异于原点的点
，点
到原点的距离记为，则
；
；
；
；
；
；
如：角的终边上一点
，则
。注意r>0
（2）在图中画出角的正弦线、余弦线、正切线；
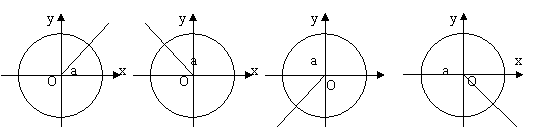
比较
，
，
，的大小关系：
。
（3）特殊角的三角函数值：
|
| 0 |
|
|
|
|
|
|
| sin | |||||||
| cos | |||||||
|
| |||||||
|
|
三、同角三角函数的关系与诱导公式：
（1）同角三角函数的关系
 |  | ||
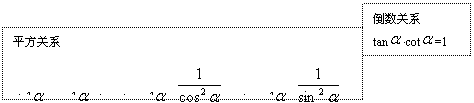作用：已知某角的一个三角函数值，求它的其余各三角函数值。
（2）诱导公式：
：
，
，
；
：
，
，
；
： ，
，
；
：
，
，
；
：
，
，
；
：
，
，
；
：
，
，
；
：
，
，
；
：
，
，
；
诱导公式可用概括为：
2K
±,-,
±,±,
±的三角函数 奇变偶不变，符号看象限 的三角函数
作用：“去负——脱周——化锐”，是对三角函数式进行角变换的基本思路．即利用三角函数的奇偶性将负角的三角函数变为正角的三角函数——去负；利用三角函数的周期性将任意角的三角函数化为角度在区间[0o,360o)或[0o,180o)内的三角函数——脱周；利用诱导公式将上述三角函数化为锐角三角函数——化锐.
（3）同角三角函数的关系与诱导公式的运用：
①已知某角的一个三角函数值，求它的其余各三角函数值。
注意：用平方关系，有两个结果，一般可通过已知角所在的象限加以取舍，或分象限加以讨论。
②求任意角的三角函数值。
步骤：
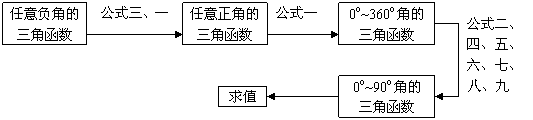
③已知三角函数值求角：注意：所得的解不是唯一的，而是有无数多个．
步骤： ①确定角所在的象限；
②如函数值为正，先求出对应的锐角
；如函数值为负，先求出与其绝对值对
应的锐角；
③根据角所在的象限，得出
间的角——如果适合已知条件的角在第二限；则它是
；如果在第三或第四象限，则它是
或
；
④如果要求适合条件的所有角，再利用终边相同的角的表达式写出适合条件的所有角的集合。
如
，则
， ；
；
_________。
注意：巧用勾股数求三角函数值可提高解题速度：（3，4，5）；（6，8，10）；（5，12，13）；（8，15，17）；
四、三角函数图像和性质
1．周期函数定义
定义 对于函数
，如果存在一个不为零的常数
，使得当取定义域内的每一个值时，
都成立，那么就把函数叫做周期函数，不为零的常数叫做这个函数的周期．
请你判断下列函数的周期
y=tan x
y=tan x y=tan x 
例 求函数f(x)=3sin 
(
的周期。并求最小的正整数k,使他的周期不大于1
注意 理解函数周期这个概念，要注意不是所有的周期函数都有最小正周期，如常函数f(x)＝c（c为常数）是周期函数，其周期是异于零的实数，但没有最小正周期．
结论：如函数
对于
，那么函数f(x)的周期T=2k;
如函数
对于，那么函数f(x)的对称轴是
2．图像
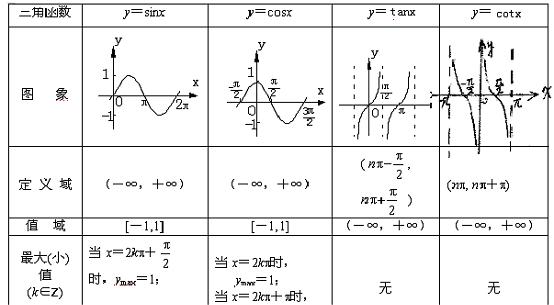
3、图像的平移
对函数y＝Asin(ωx＋j)＋k (A＞0, ω＞0, j≠0, k≠0),其图象的基本变换有：
(1)振幅变换（纵向伸缩变换）：是由A的变化引起的．A＞1,伸长；A＜1,缩短．
(2)周期变换(横向伸缩变换)：是由ω的变化引起的．ω＞1，缩短；ω＜1,伸长．
(3)相位变换(横向平移变换)：是由φ的变化引起的．j＞0,左移；j＜0，右移．
(4)上下平移(纵向平移变换): 是由k的变化引起的．k＞0, 上移；k＜0,下移
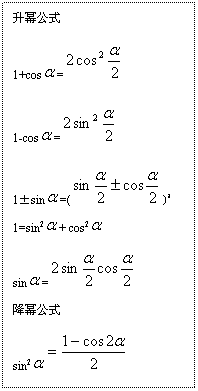
四、三角函数公式：
 | ||||
 | ||||
 | ||||
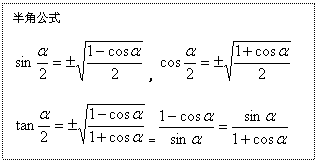三倍角公式：
；
；
五、三角恒等变换：
三角变换是运算化简的过程中运用较多的变换，提高三角变换能力，要学会创设条件，灵活运用三角公式，掌握运算，化简的方法和技能．常用的数学思想方法技巧如下：
（1）角的变换：在三角化简，求值，证明中，表达式中往往出现较多的相异角，可根据角与角之间的和差，倍半，互补，互余的关系，运用角的变换，沟通条件与结论中角的差异，使问题获解，对角的变形如：
①
是的二倍；
是的二倍；是的二倍；是
的二倍；
是
的二倍；是
的二倍；
是
的二倍。
②
；问：
；
；
③
；④
；
⑤
；等等
（2）函数名称变换：三角变形中，常常需要变函数名称为同名函数。如在三角函数中正余弦是基础，通常化切、割为弦，变异名为同名。
（3）常数代换：在三角函数运算，求值，证明中，有时需要将常数转化为三角函数值，例如常数“1”的代换变形有：
（4）幂的变换：降幂是三角变换时常用方法，对次数较高的三角函数式，一般采用降幂处理的方法。常用降幂公式有：
；
。降幂并非绝对，有时需要升幂，如对无理式
常用升幂化为有理式，常用升幂公式有：
；
；
（5）公式变形：三角公式是变换的依据，应熟练掌握三角公式的顺用，逆用及变形应用。
如：
； 
；
；
；
；
；
；
；
；
=
；
=
；
（其中
；）
；
；
（6）三角函数式的化简运算通常从：“角、名、形、幂”四方面入手；
基本规则是：切割化弦，异角化同角，复角化单角，异名化同名，高次化低次，无理化有理，和积互化，特殊值与特殊角的三角函数互化。
如：
；
；
；
；推广：
；推广：