第一课时 1.4.1 正弦函数、余弦函数的图象
教学要求：熟练把握正弦、余弦函数图象的形状特征.
教学重点：正弦、余弦函数的图象作法及其形状特征.
教学难点：正弦函数图象的作法、正弦函数和余弦函数图象间的关系.
教学过程：
一、复习准备：
1. 讨论：实数集与角的集合之间可以建立一一对应关系，而一个确定的角又对应着唯一确定的正弦（余弦）值. 由这个对应法则所确定的函数
（或
）叫做正弦函数（或余弦函数），其定义域是
.
2. 提问：如何作出正弦函数的图象？（利用正弦线可以画出较精确的正弦函数图象）
二、讲授新课：
1. 教学正弦函数图象的画法：
① 提问：正弦线的意义？(正弦线是与单位圆有关的平行于坐标轴的有向线段，它是正弦函数的几何表示)
② 用正弦线画出正弦函数的图象（边讲边画）：
第一步：先作单位圆，把⊙O1十二等分（当然分得越细，图象越精确）；
第二步：十二等分后得0,
, 
,
,…2p等角，作出相应的正弦线；
第三步：将x轴上从0到2p一段分成12等份(2p≈6.28)，若变动比例，今后图象将相应“变形”；
第四步：取点，平移正弦线，使起点与
轴上的点重合；
第五步：用光滑的曲线把上述正弦线的终点连接起来，得y=sinx，xÎ[0,2p]的图象；
第六步： 由终边相同的三角函数性质知y=sinx ，xÎ[2kp,2(k+1)p] kÎZ,k¹0的图象与函数y=sinx， xÎ[0,2p]图象相同，只是位置不同——每次向左（右）平移2p单位长.
③ 用“五点（画图）法”作正弦函数图象时，要抓住关键的五个点：(0,0) (,1) (p,0) (
,-1) (2p,0). （通过学生观察正弦函数的图象，找出体现图象形状特征的点，再来讲“五点法”.）
“五点法”的优点是方便，但精确度不高，熟练后才使用.
2. 教学余弦函数图象的画法：
由于
，而
的图象可以通过将正弦函数
的图象向左平移
个单位长度得到，因此只需将函数的图象向左平移个单位长度就可以得到函数
的图象.
思考：如果用“五点法”作余弦函数的图象，则应抓住哪五个关键点？
3. 例题讲解：
例、画出下列函数的简图：
（1）
；（2）
. （教师引导→学生板书）
4、小结：正弦曲线、余弦曲线的几何画法、“五点法”画法及正弦、余弦函数图象的形状特征.
三、巩固练习：
1. 在同一直角坐标系中，分别作出函数
、
的草图.
2. 讨论如何用“五点法”画
的图象？（方法：取
）
3. 作业：教材P52 第1题
第二课时 1.4.2 正弦函数、余弦函数的性质（一）
教学要求：掌握正弦函数、余弦函数的周期性、奇偶性和最大值、最小值，会求形如
（或
）的函数的最小正周期，并会利用正弦、余弦函数的最大值、最小值求相关函数的值域.
教学重点：正弦函数、余弦函数的性质（包括周期性、奇偶性和最大值、最小值）.
教学难点：正弦函数、余弦函数性质的应用.
教学过程：
一、复习准备：
1. 提问：①函数
的图象与函数的图象有什么关系？（学生经思考后回答）②如何作出函数
的图象？（学生板书→教师总结方法）
2. 讨论：由正弦、余弦函数的图象有哪些特征？
二、讲授新课：
1. 教学正弦、余弦函数的周期性：
① 正弦函数值具有“周而复始”的变化规律，这一点可以从正弦线的变化规律中看出，还可以从诱导公式
中得到反映，即当自变量的值增加
的整数倍时，函数值重复出现.
②周期函数的定义：对于函数
，如果存在一个非零常数
，使得当取定义域内的每一个值时，都有
，那么函数就叫做周期函数，非零常数叫做这个函数的周期.
（周期函数的周期不唯一，
都是它的周期，所有周期中最小的正数就叫做它的最小正周期）
③正弦函数、余弦函数都是周期函数，
都是它们的周期，最小正周期是.
例1：求下列函数的周期：
（1）
；（2）
；（3）
.
（师生共析→教师板书→学生观察→总结规律：这些函数的周期与解析式中哪些量有关？）
④结论：形如（或）的函数的最小正周期
.
2. 教学正弦函数、余弦函数的奇偶性：
由图象观察，结合诱导公式
知，正弦函数是奇函数，余弦函数是偶函数.
3. 教学正弦函数、余弦函数的最大值、最小值：
观察图象发现，正弦曲线、余弦曲线均有最高点和最低点，即函数值都有最大值、最小值.
例2：下列函数有最大值、最小值吗？如果有，请写出取最大值、最小值时的自变量的集合，并说出最大值、最小值分别是什么？
（1）
；（2）
.
（教师引导→学生分析→教师总结并板书）
练习：教材P45 第3题
4、小结：正弦、余弦函数的周期性、奇偶性、最大值、最小值，数形结合思想.
三、巩固练习：
1.作出函数的图象，1）解不等式：
；2）求
时
的值域.
2.作业：教材P52 第2题
第三课时 1.4.3 正弦函数、余弦函数的性质（二）
教学要求：掌握正弦函数、余弦函数的单调性，并会运用单调性，比较三角函数值的大小，求三角型函数的单调区间.
教学重点：正弦函数、余弦函数的单调性.
教学难点：正弦函数、余弦函数单调性的应用.
教学过程：
一、复习准备：
1. 练习：求出下列函数的最小正周期，并说明下列函数是否有最大值、最小值，如果有，请写出取最大值、最小值时的自变量的集合.
（1）
；（2）
.
2. 提问：如何比较
与
的大小？
二、讲授新课：
1. 教学正弦、余弦函数的单调性：
先在正弦函数的一个周期的区间上（如
）讨论它的单调性，再利用它的周期性，将单调性扩展到整个定义域.
观察图象可得，①正弦函数在每一个闭区间
（
）上都是增函数，其值从－1增大到1；在每一个闭区间
（）上都是减函数，其值从1减到－1.②余弦函数在每一个闭区间
（）上都是增函数，其值从－1增大到1；在每一个闭区间
（）上都是减函数，其值从1减到－1.
2. 教学正弦、余弦函数的应用：
例1：利用三角函数的单调性，比较下列各组数的大小：
（1）与；（2）
；（3）
.
（学生口答第1小题→学生板书第2小题→师生共析第3小题→教师板书第3小题）
练习：教材P45 第5题
例2：求函数
的递增区间.
（师生共析→教师板书→小结：整体代入，解不等式→变式：解不等式
）
练习：①求出上例中函数的单调递减区间. ②教材P45 第6题
例3：求函数
的递增区间.
（师生共析→学生板书）
3. 小结：正弦、余弦函数的单调性；整体代入法求单调区间.
三、巩固练习：
1. 练习：教材P52 第1（2）题
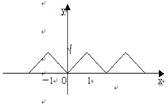
2. 已知函数
的图象如图所示，试回答下列问题：
（1）求函数的周期性；（2）画出函数
的图象；
（3）你能写出函数的解析式吗？
3. 作业：教材P52 第5题
第四课时 1.4.4 正切函数的性质和图象
教学要求：掌握正切函数的性质，学会画正切函数的图象，深化研究函数性质的思想方法.
教学重点：正切函数的性质和图象.
教学难点：正切函数性质的应用.
教学过程：
一、复习准备：
1. 复习：正弦、余弦函数的图象和性质；研究正弦、余弦函数性质的方法？
2. 提问：能否依照研究正弦、余弦函数性质的方法来研究正切函数的性质和图象？
二、讲授新课：
1. 教学正切函数的性质：
① 定义域：
；
② 周期性：由诱导公式
可知，正切函数是周期函数，最小正周期是
.
③ 奇偶性：由诱导公式
可知，正切函数是奇函数.
④ 单调性：由正切线的变化规律可以看出，正切函数在
内是增函数，又由正切函数的周期性可知，正切函数在开区间
内都是增函数.
⑤ 值域：正切函数的值域是实数集R.
2. 教学正切函数图象的画法：
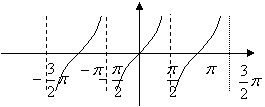
① 利用正切线画出函数
的图象，再根据正切函数的周期性，把上述图象向左、向右扩展，就可以得到正切函数
且
的图象，我们把它叫做正切曲线.
② 分析正切函数的图象特征. ③由图象分析正切函数的性质.
例1：求函数
的定义域、周期和单调区间. （练→方法→变式：解
）
例2：利用正切函数的单调性比较下列各组数中两个正切值的大小：
（1）
与
；（2）
3. 小结：正切函数的图象和性质，整体思想求定义域与单调区间，正切线分析思路.
三、巩固练习：
1. 练习：教材P50 第2、4题 2. 作业：教材P52 第6、7、8题