倍角的三角函数
一、选择题
1、已知
（
）
A．
B．
C．
D．
2、化简
的结果是（
）
A．1 B．－1 C．0 D．2
3、sin6°·cos24°·sin78°·cos48°=（ ）
A．
B．
C．
D．
4、若
（
）
A．-2cosθ B．2cosθ C．2sinθ D．－2sinθ
5、已知
，且α是第二象限角，则
（
）
A．
B．5
C．5或
D．－5或
6、化简
（
）
A．2sin4 B．2sin4－4cos4 C．4cos4－2sin4 D．－2sin4
7、
（
）
A．-1 B．0 C．1 D．2
8、若sinαsinβ＋cosαcosβ=0，则sinαcosα＋sinβcosβ=（ ）
A．-1 B．0
C．1 D．
9、已知cos(α＋β)·cos(α－β)=
则cos2α－sin2β=（
）
A．
B．
C． D．
10、若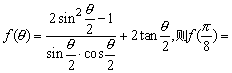
（
）
A．0 B．2 C．-2 D．-4
二、填空题
窗体底端
11、若
则cos4A=________________.
12、已知θ为第二象限角，且
______________________.
三、解答题
13、求值：
.
14、已知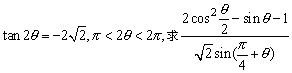
的值.
15、已知sinθ＋sin2θ=a,cosθ＋cos2θ=b.求证：(a2＋b2)(a2＋b2－3)=2b.
答案：一、DCABA DCBCD
提示：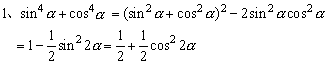 
2、原式=
3、原式=
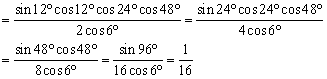
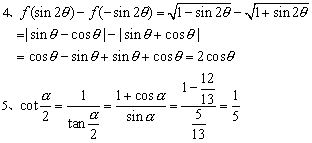
6、原式=2sin4－cos4＋2cos4=2(cos4－sin4)－2cos4=－2sin4
7、原式=
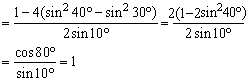
8、由已知得cos(α－β)=0，即a－β=kπ＋
.
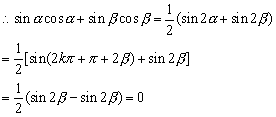
9、cos(α＋β)cos(α－β)=cos2αcos2β－sin2αsin2β=cos2α－sin2β
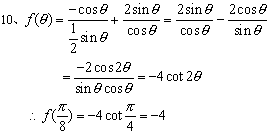
二、11、
提示：由已知条件平方得
12、
提示：由已知得
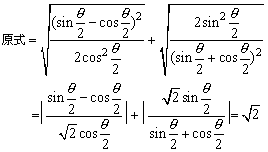
三、13、解答：原式 =
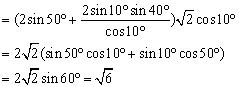
14、解答：原式 =
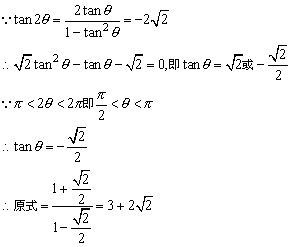
15、解答：∵ a=sinθ＋sin2θ b=cosθ＋cos2θ
∴a2＋b2=(sinθ＋sin2θ)2＋(cosθ＋cos2θ)2=2＋2cosθ
∴a2＋b2－3=2cosθ－1
∴(a2＋b2)( a2＋b2－3)=(2＋2cosθ)(2cosθ－1)
=2(2cosθ－1＋2cos2θ- cosθ)
=2(2cos2θ－1＋cosθ)
=2(cos2θ＋cosθ)
=2b