高一下学期数学
周测试题（一）
时间：120分钟 满分：160分
第I卷(共50分)
一. 选择题(本大题满分50分,每小题5分)本大题共有10小题，每题都给出代号为A、B、C、D的四个结论，其中有且只有一个结论是正确的.
1．下列命题中正确的是
A.第一象限角一定不是负角
B.小于90
的角一定是锐角
C.钝角一定是第二象限的角 D.终边相同的角一定相等
2.
A. 
B.
C. 
D.
3.已知
是第四象限角，则
是
（ ）
A.第一或第二象限角 B.第一或第三象限角
C.第一或第四象限角 D.第二或第四象限角
4.一钟表的分针长10 cm，经过35分钟，分针的端点所转过的长为（ ）
A．70 cm
B．
cm
C．(
)cm D．
cm
5.若角的终边落在直线y=2x上，则sin的值为（ ）
A. 
B. 
C. 
D.
6．已知是三角形的一个内角,且
,则这个三角形是(
)
A．锐角三角形 B．钝角三角形
C．不等腰的直角三角形 D．等腰直角三角形
7.
等于
（ ）
A．sin2－cos2 B．cos2－sin2
C．±（sin2－cos2） D．sin2+cos2
8.要得到函数
的图象，只需将
的图象（ ） A．向右平移
B．向左平移
C．向右平移
D．向左平移
9.设
的最小正周期是（ ）
A．
B．
C．
D．
10.函数
的图象的一个对称轴方程是（ ）
A．
B．
C．
D．
|
| 得分 | 阅卷人 |
|
|
|
第
卷(共110分)
| 得分 | 阅卷人 |
|
|
|
二．本题满分30分.、填空题：本题共有6小题．只要求直接填写结果，每题填对得5分，否则一律是零分.
11.
12.
.
13.
.
14.
.
15.函数y＝cos(－2x)的单调递增区间是
.
16.已知
，且
,则
=
.
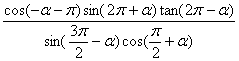三.解答题：本题共有7小题，要求写出解答过程和演算、证明步骤.本题满分80分.
| 得分 | 阅卷人 |
|
|
|
17.（本题满分10分）
| 得分 | 阅卷人 |
|
|
|
18. （本题满分10分）求证：
| 得分 | 阅卷人 |
|
|
|
19.（本题满分10分）已知
求
的值．
| 得分 | 阅卷人 |
|
|
|
20.（本题满分10分）求函数
，
的值域。
| 得分 | 阅卷人 |
|
|
|
21.（本题满分12分）已知一扇形的周长为c(c＞0)，当扇形的弧长为何值时，它有最大面积？并求出面积的最大值．
| 得分 | 阅卷人 |
|
|
|
22.（本题满分14分） 已知y＝Asin(ωx＋φ)，(A＞0, ω＞0,
)的图象过点P(,0)图象上与点P最近的一个顶点是Q(,5)．
(1)求函数的解析式；
(2)求使y≤0的x的取值范围．
| 得分 | 阅卷人 |
|
|
|
23.（本题满分14分）已知某海滨浴场海浪的高度y米是时间t（
，单位：小时）的函数，记作y=f(t).下表是某日各时的浪高数据：
| t(时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y（米） | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1 | 0.5 | 0.99 | 1.5 |
经过长期观测y=f(t)的曲线可近似地看成是函数y=Acos
t+b
（1）根据以上数据求函数y的最小正周期T，振幅A及解析式
（2）依据规定，当海浪高度高于1米时才对冲浪爱好者开放，请依据（1）的结论，判断一天内的上午8：00时至晚上20：00时之间，有多少时间可供冲浪者进行运动？