高中一年级数学期末教学质量检测
本试卷分为第I卷（选择题）和第II卷（非选择题）两部分。第I卷共60分，第II卷共90分，全卷满分共150分，考试时间120分钟。第I卷用铅笔答在答题卡上，第II卷用钢笔或圆珠笔直接答在试题卷上。考试结束后将本试卷和答题卡一并交回。
第I卷（选择题 共60分）
一、选择题：本大题共12小题，每小题5分，共60分。在所给的四个选项中，只有一项是正确的。
1.如果S={1，2，3，4，5}，M={1，3，4}，N={2，4，5}，那么（CSM）∩（CSN）等于
A.{4} B.{1，3} C.{2，5} D.φ
2.设p、q是两个命题，那么“p且q”为真命题是“p或q”为真命题的
A.充分但不必要条件 B.必要但不充分条件
C.充要条件 D.既不充分又不必要条件
3.与函数y=
有相同图像的一个函数是
A.－
B. x
C. －x
D.x2
4.如果A={x x－1≥a}，B={x x+1<4}，且A∩B=φ，那么a的取值区间是
A.
B.
C. (6，+∞) D. 
5.已知函数f (x) = x2 + bx + c，f (－1) = f (3)，则
A. f (1)>c> f (－1) B. f (1)<c< f (－1)
C. c> f (－1) > f (1) D. c< f (－1) < f (1)
6.某种细胞在培养过程中每20分钟分裂一次（一个分裂成两个），经过3小时，1个细胞可分裂为
A.511个 B.512个 C.1023个 D.1024个
7.若0<a<1，则关于x的方程ax = log a x 的解的个数为
A.0个 B.1个 C.2个 D.3个
8.已知数列{an}为等比数列，前三项为a，
和
，则T n= a12+ a22+…+ an2等于
A. 
B. 
C. 
D.
9.数列{an}的前n项和S n = n－a2，则当n∈N*且n≥2时一定有
A. n an < n a1 <S n B. S n< n an < n a1 C. n an < S n< n a1 D. n a1 <S n< n an
10.方程ax2 + 2x +1=0至少有一个负的实数根的充要条件是
A.0<a≤1 B. a<0 C. a≤1 D. 0<a≤1或a<0
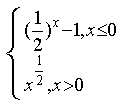
11.设函数f(x)= 若f(m) －1>0，则m的取值区间是
A.（－1，1） B.（1，+∞）
C.（－∞，－1）∪（0，+∞） D. （－∞，－1）∪（1，+∞）
12.要得到函数y=log 3 (x+1)的图像，可以先将函数y=3 x的图像
A.先向左平移1个单位 B. 先向右平移1个单位
C.先向上平移1个单位 D. 先向下平移1个单位
再作关于直线y=x对称的图像。
高中一年级数学期末教学质量检测
第II卷（非选择题 共90分）
注意：答卷前将密封线内的项目填写清楚，密封线内不要答题。
| 第I卷 | 第II卷 | 总分 | 总分人 | |||||||
| 题号 | 一 | 二 | 三 | |||||||
| 17 | 18 | 19 | 20 | 21 | 22 | |||||
| 得分 | ||||||||||
二、填空题：本大题共4小题，每小题4分，共16分。把正确答案填在题中横线上。
13.已知命题：“若a ，b ，c成等比数列，则b2 =ac”。这个命题的逆命题、否命题、逆否命题中真命题的个数为____________。
14.利用换底公式：
，计算log225·log34·log59=___________。
 |
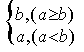15.定义运算：a
b=
则函数f(x)=2 –x
2 x的值域为_________________
16.对于函数f(x)= 
定义域中任意的x1，x2（x1≠x2），有如下结论：
①f(x1+x2)= f(x1)·f(x2) ②f(x1)·f(x2)= f(x1)+f(x2)
③
④
上述结论中正确的所有序号是_______________。
三、解答题：本大题共6小题，共74分；解答应写出文字说明、证明过程或演算步骤。
17.（本小题满分12分）求函数
的定义域、值域及单调区间。
18. （本小题满分12分）有四个正数，前三个数成等差数列，其和为48；后三个数成等比数列，其最后一个数为函数y=21+4x－x2的最大值。求这四个数。
19. （本小题满分12分）已知函数f(x)=a·b x的图像经过点A（1，
）和B（2，
）。
（1） 求函数f(x)的解析式；
（2）
记
,S n是数列{a n}的前n项和，求S 30 ；
（3） 在（2）的条件下，解关于n的不等式：a n ·S n≤0。
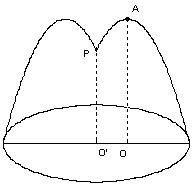
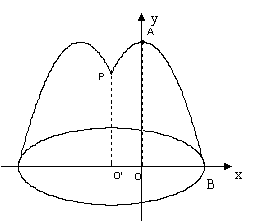
20. （本小题满分12分）如图，花坛圆形水池中央有一喷泉。水管O’P的高为1m，水从喷头P喷出后呈抛物线状，先向上至最高点后落下。若最高点A距水面2m，P与抛物线对称轴OA相距1m。
（1） 求花坛圆形水池半径的最小值；
（2） 如果要求喷出的水不落在水池之外，同时水池面积又不至于过大，那么在圆形水池直径的四个可选值：2.5m、4m、5m和6m中，最合算的是哪一个？请说明理由。
 |
21. （本小题满分12分）设f(x)=e x +e – x，g(x)=e x －e – x。
（1）
利用函数单调性的定义，判断f(x)在
上的单调性；
（2）
令
，求h(x)的反函数h- 1(x)。
22. （本小题满分14分）已知等比数列{x n}的各项为不等于1的正数，数列{y n}满足：
（a>0且a≠1），y 5 =15，y 8=9。
（1） 证明数列{y n}为等差数列；
（2） 数列{y n}的前多少项之和最大，最大值为多少？
（3） 试判断，是否存在正整数M，使得当n>M时，x n>1恒成立？若存在，求出相应的M；若不存在，请说明理由。
期末教学质量检测
数学参考答案 2006.1
一、选择题：DACBB BCACC DD
二、填空题
13. 1； 14.8； 15. 
； 16.②③④
三、简答题
17.解：由
得0<x<1
2分
∴函数
的定义域是(0,1)
4分
∵0<x－x2=－
∴
≥
=2
6分
∴函数的值域为
8分
令u=
x∈（0，1）
u=在
上是增函数，在
上是减函数 10分
由复合函数单调性知，在上是减函数，在上是增函数
12分
18.解：设这四个数分别为a1，a2，a3，a4， 1分
则a1+a2+a3=48 ∴3 a2=48 a2=16 4分
又y=21+4x－x2=
∴a4=25 7分
∵a4= a2·q2
∴q=
（q>0）
9分
∴a3= a2·q=20，a1=2 a2－a3=12 11分
故这四个数为12，16，20，25 12分
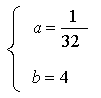
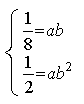19.解：（1）∵函数f(x)=a·b x的图像经过点A（1，）和B（2，），
∴ 解得 2分
∴
4分
（2）
即a n=2n－5=－3+2(n－1)，
∴数列{a n}是首项为a 1=－3，公差为2的等差数列。 6分
∴
。 8分
（3）
9分
∵
∴所求解的不等式为
解得
10分
又∵n∈N* ∴n=3,4
故不等式a n ·S n≤0的解集为{3，4} 12分
20.（1）建立如图所示的平面直角坐标系， 1分
设左侧抛物线的方程为
y=ax2+2，(－1≤x≤x B) 3分
由题意知：点P的坐标为(－1，1)，
顶点A（0，2）
∴1=a+2 ∴a=－1
于是抛物线方程为y=－x2+2 4分
令y=0 可得x=±
∴B的坐标为（，0） 6分
于是水池半径应大于或等于1+，
故花坛水池半径的最小值为1+，
8分
（2）水池直径≥2（1+）（m）
而2（1+）≈4.8
10分
故应选水池直径为5m合算。 12分
注：建立其它坐标系解正确者给相应的分。
21.（1）设x1<x2≤0 1分
f(x1)－f(x2)= （
）－（
）
=（
）+（
）
=（）+
=（）（1－
）
=（）
4分
∵x1<x2≤0，∴
，∴<0，
又e>1 ∴0<
<1，0<
≤1，∴
－1<0，>0
∴f(x1)－f(x2)>0 即f(x1)> f(x2) 5分
∴f(x)在上单调递减。
6分
（2）=
x∈R
7分
设y==1－
∴=1－y，显然1－y≠0，∴
=
∴
=－1=
=
9分
∵>0
∴>0 ∴－1<y<1
11分
于是2x=
即x=
故h(x)的反函数h- 1(x)= 
，x∈(－1，1)
12分
22.(1)证明：据已知（a>0且a≠1）得
y n+1－y n =
2分
设等比数列{x n}的公比为q，则
。
∴y n+1－y n =
（常数）
故数列{y n}为等差数列。 4分
（2）设等差数列{y n}的公差为d，则
d=
5分
又
得y1=23。
∴y n =23+（n－1）·（－2）=25－2n， 6分
令y n =25－2n≥0，解得
，n∈N*。
∴S12最大，S12=
故前12项之和最大，最大值为144。 8分
（3）由（2）知：－2=2 ∴=－1
∴
（a>0且a≠1）。
y 1 =23=2
∴
。
10分
当a>1时，要x n>1，即
>1，得
>0。
解得n<
，此时要使n>m时，x n>1恒成立，这样的正整数M不存在 12分
当0<a<1时，要x n>1，即>1，得<0，即n>。
此时，存在M=12，当n>12时，x n>1恒成立。 14分