第一课时：1.2.1 任意角的三角函数（一）
教学要求：掌握任意角的三角函数的定义；已知角α终边上一点，会求角α的各三角函数值.
教学重点：熟练求值.
教学难点：理解定义.
教学过程：
一、复习准备：
1. 用弧度制写出终边在下列位置的角的集合：坐标轴上； 第二、四象限
2. 锐角的三角函数如何定义？
3. 讨论：以上定义适应任意角的三角函数吗？如何定义？
二、讲授新课：
1. 教学任意角的三角函数的定义：
① 讨论：锐角α的终边交单位圆于点P (x,y)的坐标与α三角函数有何关系？
→ 推广：任意角
② 定义：设α是一个任意大小的角，角α的终边与单位圆交于点P (x, y),
则sinα＝y，cosα＝x，tanα＝
.
② 讨论：与点P的位置是否有关？
α与2kπ＋α的三角函数值有何关系？
当α的终边落在x轴、y轴上时，哪些三角函数值无意义？
任何实数是不是有三角函数值？
三个三角函数的定义域情况是怎样的？
2. 教学例题：
① 出示例1：求下列各角的正弦、余弦、正切值
3π、 －2π、 
、 －
讨论求法→试求（学生板演）→订正→小结：画终边与单位圆，求交点，求值.
② 思考：已知角终边上任一点P (x, y)，如何求它的三角函数值呢?
结论：先求
；再按公式
、
、
.
③ 出示例2：已知角α的终边过点P(-2,-4)，求α的正弦、余弦和正切值.
（学生试求→订正→小结解法：先求r，再按定义求. ）
④ 讨论：正弦、余弦、正切值在各个象限的符号情况？
⑤ 讨论：终边相同的角同一三角函数的值有何关系？
结论：
，
， 
，其中
．
作用：把任意角的三角函数值问题转化为0～2π间角的三角函数值问题.
⑥ 练习：求下列各角的正弦、余弦和正切值：
、－
.
3. 小结：单位圆定义任意角的三角函数；由终边上任一点求任意角的三角函数；各象限的符号情况；诱导公式（一）.
三、巩固练习：
1. 已知角α的终边在直线y＝2x上，求α的正弦、余弦和正切值.
2. 口答下列各特殊角的正弦、余弦、正切值：0°、90°、180°、270°、360°.
3. 已知点
，在角α的终边上，求
、
、
的值
4. 作业：书P17 1、2、3题.
第二课时：1.2.1 任意角的三角函数（二）
教学要求：掌握三角函数的符号，灵活运用诱导公式（一），把求任意角的三角函数值转化为求0°～360°间的三角函数值.
教学重点：灵活运用诱导公式.
教学难点：理解转化.
教学过程：
一、复习准备：
1. 提问：三个三角函数的定义、定义域及在各个象限的符号情况怎样？（填表形式）
2. 在0～2π或0°～360°间求出与下列终边相同的角：
750°、
、－
、－1020°
二、讲授新课：
1. 教学三角函数值的符号：
① 讨论：各个象限的符号情况？
② 出示例：判别下列各三角函数值的符号，然后用计算器验证.
sin250°、cos（－
）、tan(－666°36’)、tan
、sin、cos1020°
（分析：如何用诱导公式（1）转化到0°～360°？→ 试练 → 订正）
③ 出示例：根据下列已知，判别θ所在象限：
sinθ>0且tanθ<0 、 tanθ×cosθ<0
（口答→分析思路）
2. 教学诱导公式的运用：
① 讨论：根据三角函数的定义，θ与2kπ＋θ的三个三角函数情况怎样？
② 提出：诱导公式一（三个）
分析作用：求任意角的三角函数转化到0～2π间求值.
③ 出示例：求下列各角的三角函数的值（正弦、余弦、正切）.
750°、、－、－1020°
（教师示例750°→学生试求其它三个→订正）
④ 练习：函数
的值域.
解法：分象限讨论，去绝对值.
变式：求
的值域.
3. 小结：三角函数的符号及诱导公式的运用；利用诱导公式一,可以把求任意角的三角函数值, 转化为0°～360°而求，或用计算器求.
三、巩固练习：
1. 已知θ∈（
,3π），求：
3
＋
的值.
2. 解方程：sinx＝－sinx
（思路：根据各象限的符号，分情况讨论）
3. 作业：教材P17 5、7题.
第三课时：用单位圆中的线段表示三角函数值
教学要求：理解正弦线、余弦线、正切线的概念，掌握作已知角α的正弦线、余弦线和正切线.
教学重点：掌握作已知角α的正弦线、余弦线、正切线.
教学难点：理解正弦线、余弦线、正切线的概念.
教学过程：
一、复习准备：
1. 什么叫单位圆？（以原点为圆心，单位长为半径作的圆）
2. 三个三角函数是怎样定义的？
|
|
D y
二、讲授新课：
1. 教学三角函数线概念：
① 定义有向线段：直线规定方向→轴；线段规定方向→有向线段；
② 讨论有向线段表示：与轴正向同为正，否则为负.
③ 练习：如图，AB＝ BA＝ OC＝ CD＝ DC＝
④ 画出下列角度与单位圆的交点P，并作x轴的垂线PM，写出PM、OM的值，并与正弦、余弦值比较： 120°、240°
⑤ 定义正余弦线：设角α的终边与单位圆交点P(x，y),过P作x轴的垂线，垂足为M，则有向线段MP为正弦线，OM为余弦线.
⑥ 练习：画出各象限终边角的正弦线、余弦线，并分析符号.
⑦ 定义正切线：过点A(1,0)作单位圆的切线，与终边或延长线交于T，则有向线段AT叫角α的正切线.
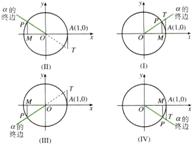⑧ 练习：画出各象限终边角的正切线，并分析符号.
2. 讨论问题：
① 讨论一：三角函数线为什么可以表示三角函数值？
先单位圆中计算得sinα=y，cosα＝x；
比较MP的长度与y、OM的长度与x；
比较MP的符号与y的符号，OM的符号与x的符号；
所以 sinα＝y＝MP， cosα＝x＝OM，
tanα＝＝
=
＝AT （由三角形相似得）
② 讨论二：α终边在坐标轴上时的正弦线、余弦线、正切线的情况？
3. 教学例题：
① 出示例：已知
，试比较
的大小.
（分析：如何通过三角函数线比较？ →
小结：利用三角函数线比大小 → 变式：
）
② 练习：利用三角函数线比较下列各组数的大小：
与
；
与
.
4. 小结：三角函数线概念与作法；三角函数线的运用.
三、巩固练习：
1. 作、
、－40°的正弦线、余弦线、正切线.
2. 利用单位圆写出符合下列条件的角x的范围： sinx=
； tanx
；
3. 作业：教材P19 第2题.
第四课时 1.2.2 同角三角函数的基本关系（一）
教学要求：掌握同角三角函数的三个基本关系式，掌握已知一个角的某一个三角函数值，求这个角的其他三角函数值.
教学重点：运用关系式.
教学难点：理解同角三角函数关系式.
教学过程：
一、复习准备：
1.提问：任意角的三个三角函数是怎样定义的？
2.提问：初中研究锐角的三个三角函数，它们有怎样的关系式？
二、讲授新课：
1. 教学同角三角函数的三个基本关系式：
① 讨论：从三个三角函数的定义，你能发现哪些三角函数有平方关系？哪些三角函数与其他三角函数有商数关系？
② 结论：平方关系
；商数关系
.
③ 讨论：利用三角函数线的定义, 如何推导同角三角函数的基本关系？
④ 讨论几个问题：
A.上述两个关系式，在一些什么情况下成立？
B.“sin
α＋cosβ＝1”对吗？
C. 同角三角函数关系式可以解决哪些问题？
（求值：已知一个角的三角函数值，求这个角的其他三角函数的值； 化简；证明）
2. 教学例题：
① 出示例1：已知cosα＝－
，并且它是第三象限的角，求sinα，tanα的值.
思考：由已知可以根据哪些关系式分别求其它三角函数值？注意什么问题？
解答→订正→小结：关系式的运用；注意符号问题；
再思考：假如没有已知所在象限，结果将怎样？假如是填空选择，有何捷径求解？
② 练习：已知sinα＝
，求cosα，tanα的值.
小结：注意符号（象限确定）；同角三基本式的运用（分析联系）；知一求二.
3. 练习：
① 若tanα=
，
，求sinα.
② 化简cosθtanθ. （化简方法：切化弦）
③ 化简下列各式：
4. 小结：① 给值求值：已知一个角的某一个三角函数值，便可运用基本关系式求出其它三角函数值. ② 化简的要求（化简后的式子，三角函数的种类最少；分母不含根式；项数最少；能求出值的求出值）
三、巩固练习：
1. 已知β的一个三角函数值，求其它三角函数值：cosβ＝
； tanβ＝－4
2. 已知tanα＝m（m≠0），求sinα，cosα的值. （分象限讨论）
3. 作业：教材P23 练习1、2、4题.
第五课时：1.2.2 同角三角函数的基本关系（2）
教学要求：能熟练运用同角三角函数的三个基本关系式，掌握已知一个角的某一个三角函数值，求这个角的其它三角函数值；能利用关系式化简三角函数式. 能够利用三角函数的基本关系式证明有关的三角恒等式.
教学重点：运用公式.
教学难点：合理选用关系式.
教学过程：
一、复习准备：
1. 根据下列条件，求角α的其它三角函数值.：sinα＝－
,α在第四象限； tanα＝2
2. 提问：同一个角的三个三角函数有哪些基本关系式？
二、讲授新课：
1. 教学例题：
① 出示例1：用多种方法证明：
＝
学生讨论证法，逐一补充完整
证法一：＝
＝…
证法二：＝
＝…
证法三、四：从右边开始，……
证法五：(1+sinx)(1-sinx)＝…
② 小结方法：由其它等式而转化（先证交叉乘积相等）；或证和（差），或证商→比较法；直接证明左边等于右边.
③ 练习：求证：sinx tanx =tanx－sinx.
④ 出示例2：已知tanα＝－，求α的其它三角函数的值；求
的值.
分析：如何运用同角三角函数基本关系式求解？
变式：如何直接求第2问？ （弦化切）
训练：
（技巧：切用分母1）
2 . 练习：
① 已知sin
=2sinβ，tan=3tanβ，求
的值.
② 已知
+
=1，求sinα+cosα的值.
3. 小结：注意象限定符号和联系关系式. 灵活运用公式，注意平方关系，切化弦；化繁为简.
三、巩固练习：
1. 已知α是第二象限角，且tan(2π+α)=
, 求cosα和sinα的值.
2. 已知
=
，求
和
的值.
3. 已知tanα=2，求下列各式的值：
； 
.
4. 作业：教材P24 11、12、13题.