高一数学第一学期期中考试试卷3

高一数学第一学期期中考试试卷3

时间：120分钟　 分值：120分

各位同学：读书改变命运，细节决定成败。希望你认真审题，仔细答题；

祝你考出好成绩！

一，选择题：（每题4分，共48分）

1，已知集合M=｛y∣y＜6　,y∈N｝，N=｛2,　3,  6｝则M∩N=

A．｛2，3，6｝ 　　　　　　　B．｛1，2，3，4，5｝

 C．｛2，3｝　 　　　　　　 D．｛0，1，2，3，4，5，6｝

2，已知集合A=｛y∣y= logx, x >1｝,B=｛y∣y=(), x >1｝，则A∩B=

A．｛y∣0<y<｝　B．｛y∣y＞0｝　C．　　 D．R

3，函数y=的定义域是

A．(－,0 )　　B．(　0, 2 ]　 C．[0,2]　　D．[ －2, 0 ]

4，以下四组函数中,表示同一个函数的是　

A．y= logx和y=2 logx　　　B．y=x和y= loga

C．y=x+1与y=　　  D．y=x－1与y=

5，函数y = log（x－1）

A．在（0, +）上是增函数　　　 B．在（0, +）上是减函数　

 C．在（1, +）上是增函数　　　 D．在（1, +）上是减函数

6．计算log（4×32）的值是

A． 23　 B．14　 C．86　　　 D．90

7，已知函数f(x)= 2mx+4若在[－2, 1]上存在x，使f(x)＝0，则实数m的取值范围为

A．[－,4]　 B．(－,－2 ] U [1,＋)　　 C． [－1,2]　　D． [－2,1]

8，函数f(x)=lnx+ 2x－6的零点必定位于的区间是

A．（1,2）  B．（2,3）　C．（3,4）  D．（4,5）

9，函数y=的值域为

A．R　　B．｛y∣y ≥ ｝　C．｛y∣y ≤｝　　 D．｛y∣0< y ≤｝

10，已知log<1,则a的取值范围是

A． 0＜a＜　B．a＜　C． ＜a＜1　 D．0＜a＜或a＞1

11，已知函数 f(x)=（）在区间 [－2,－1]上的最大值是

A．1 　B．9　　C．27　　D．

12，幂函数 f(x)=x的图象一定不经过

A．　第一象限　 B．第二象限　C．　第三象限　　D．第四象限

请把选择题的答案填在下面的方格内（填在其它地方不得分）

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案

二、填空题：（每题4分，共32分）

13，某树林现有木材30000立方米，如果每年增长5%，经过x年，树林中有木材

y立方米，那么x与y的函数关系式为 　　　　　　　

14，函数f(x)= log（2x －x²）的单调递增区间是　　　　　　

15，函数f(x)= log(x－2)－1(a>0且a≠1)的图象恒过定点为　　　　　　　　 

16，计算：log5 •log7•log16=　　　；17．若5=a，5=b,则5=　　　　 

18．长为4，宽为3的矩形，当长增加x，且宽减少时面积最大，此时x=　　　，面积S=　　　　　　　19．计算：+－（）＝　　　　　

20． 已知幂函数y=f(x+2)是偶函数，则符合条件的一个函数f(x)的

解析式为　　　　　　　　　  （只需写出一个符合条件的函数解析式）

三、解答题：（共40分）

21．计算（或求值）：（10分，每小题5分）

（1）2××　　　　　　　　（2）已知log[log(logx)] =0,求x的值　

22，已知A=｛x∣X²－ax＋a²－19=0｝,　B=｛x∣x²－5x＋6=0｝,　C=｛x∣x²＋2x－8=0｝,若A∩B=B∩C,求a的值。（7分）

23．设0≤x≤2，求函数y=4－3 • 2+ 5 的最大值和最小值。（7分）

24．当k为何值时，关于x的一元二次方程kx+kx+k－3=0的两根满足x₁<1<x_2.

（7分）

25，通过

研究学生的学习行为，心理学家发现，学生的接受能力依赖于老师引入概念和描述问题所用的时间。讲座开始时，学生的兴趣激增，中间有一段不太长的时间，学生的兴趣保持较理想状态，随后学习的注意力开始分散。分析结果和实验表明，用f(x)表示学生掌握和接受概念的能力，x表示提出和讲授概念的时间（单位：分钟），可有以下公式：

f(x)=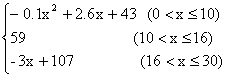

（1）开讲后多少分钟，学生的接受能力最强（即f(x)最大）？能维持多长时间？

（2）开讲后5分钟与开讲后20分钟比较，学生的接受能力何时强一些？

（3）有一道数学难题，需要55的接受能力以及13分钟时间，老师能否及时在学生一直达到所需接受能力的状态下讲完这道数学难题？（9分，每小题3分）