高一数学科第二学期期末统一考试
数学科试卷
本试卷分第I卷(选择题)、第II卷(非选择题)两部分. 共100分,考试时间100分钟.
第I卷(选择题共40分)
注意事项:
1. 答第I卷前,考生务必将自己的姓名、统考考号、座位号、考试科目用铅笔涂写在答题卡上.
2. 每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试题上.
3. 可以使用科学型计算器.
4. 考试结束,将答题卡与第Ⅱ卷交回.
一、选择题(本大题共10小题,每小题4分,共40分. 在每小题给出的四个备选项中,只有一项是符合题目要求的.)
1.
![]() =
=
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
2. 把二进制数110011(2)化为非二进制数,下列结果不正确的是
A. 51 B. 201(5) C. 123(6) D. 36(8)
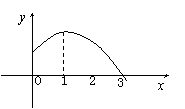 3. 函数
3. 函数![]() 的部分图象如右图,则
的部分图象如右图,则![]() 、
、![]() 可以取的一组值是
可以取的一组值是
A.
![]()
B.
![]()
C.
![]()
D. ![]()
4.
已知![]() ,且向量
,且向量![]() 与
与![]() 平行,则k=
平行,则k=
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
5.
已知![]() ,则
,则![]() 的值是
的值是
 A.
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
6.
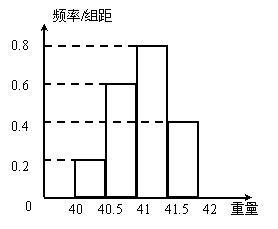
某工厂生产的200件产品的重量(单位:kg)的频率分布直方图如右图所示,则重量在![]() 的产品大约有
的产品大约有
A. 160件 B. 120件
C. 80件 D. 60件
 7. 已知
7. 已知![]() 是第四象限角,则
是第四象限角,则![]() 可化简为
可化简为
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
8. 如果右边所给出的程序执行后输出的结果是720,那么
在程序until后面的“条件”应为
A. i > 9 B. i <7
C. i <=8 D. i<8
9. 某商店购进12件同品牌的衣服,其中10件是正品,其余2件是次品,从中无放回地任取2件,则取出的2件衣服中,至少有1件是次品的概率是
A. ![]() B.
B.
![]() C.
C.
![]() D.
D. ![]()
10.
将最小正周期为![]() 的函数
的函数![]() 的图象向左平移
的图象向左平移![]() 个单位,得到偶函数图象,则满足题意的
个单位,得到偶函数图象,则满足题意的![]() 的一个可能值为
的一个可能值为
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
第二学期期末统一考试
数学科试卷
第II卷(非选择题共60分)
| 题 号 | 二 | 15 | 16 | 17 | 18 | 19 | 总分 | 总分人 | 复分人 |

二、填空题(本大题共4小题,每小题4分,共16分,把答案填在题中的横线上)
11. 若向量![]() 与
与![]() 垂直,则
垂直,则![]() = .
= .
12. 已知![]() ,则
,则![]() .
.
13. 某校1000名学生中,O型血有400人,A型血有250人,B型血有250人,AB型血有100人,为了研究血型与性格的关系,按照分层抽样的方法从中抽取样本. 如果从A型血中抽取了10人,则从AB型血中应当抽取的人数为 .
14. 由物理中矢量运算及向量坐标表示与运算,我们知道:
(1)两点等分单位圆时有相应关系式为:![]() ;
;
(2)四点等分单位圆时有相应关系式为:![]() ,
,
![]() .
.
由此我们可以推测,三点等分单位圆时的相应关系式为 ,
.
三、解答题(共5个题. 15、16、17题各8分, 18、19题各10分,合计44分)
|
(1)求![]() 的值; (2)求
的值; (2)求![]() 的最大值及对应的
的最大值及对应的![]() 值.
值.
|
(1)若![]() 的夹角
的夹角![]() 为
为![]() ,求
,求![]() ;(精确到0.001)
;(精确到0.001)
(2)若![]() 与
与![]() 垂直,求
垂直,求![]() 与
与![]() 的夹角
的夹角![]() .
.
|
(1)若抽奖规则是从一个装有6个红球和4个白球的袋中无放回地取出2个球,当两个球同色时则中奖,求中奖概率;
(2)若甲计划在9:00~9:40之间赶到,乙计划在9:20~10:00之间赶到,求甲比乙提前到达的概率.
|
(1)画出函数![]() 在长度为一个周期的闭区间上的简图;
在长度为一个周期的闭区间上的简图;
(2)将函数![]() 的图象作怎样的变换可得到
的图象作怎样的变换可得到![]() 的图象?
的图象?
(3)设函数![]() ,求
,求![]() 的周期、单调递减区间.
的周期、单调递减区间.

|
| t(时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y(米) | 1.0 | 1.4 | 1.0 | 0.6 | 1.0 | 1.4 | 0.9 | 0.4 | 1.0 |
(1)试画出散点图;
(2)观察散点图,从![]() 、
、![]() 、
、![]() 中选择一个合适的函数模型,并求出该拟合模型的解析式;
中选择一个合适的函数模型,并求出该拟合模型的解析式;
(3)如果确定当浪高不低于0.8米时才进行训练,试安排白天内进行训练的具体时间段.
第二学期期末统一考试
数学科试卷参考答案
一、BDCAB CBDDA
二、11. ±2 12.
![]() 13. 4
13. 4
14. ![]() ,
,![]()
三、
15.解:(1)![]() . ……(1分)
. ……(1分)
![]() . ……(3分)
. ……(3分)
(2)![]() ……(4分)
……(4分)
![]() . ……(5分)
. ……(5分)
当![]() ,即
,即![]() 时, ……(7分)
时, ……(7分)
![]() . ……(8分)
. ……(8分)
16. 解:(1)由![]() , ……(2分)
, ……(2分)
得![]() .……(3分)
.……(3分)
∴ ![]() . ……(4分)
. ……(4分)
(2) ∵ ![]() 与
与![]() 垂直, ∴
垂直, ∴ ![]() . ……(5分)
. ……(5分)
即![]() , ∴
, ∴ ![]() . ……(6分)
. ……(6分)
又 ![]() , ……(7分)
, ……(7分)
∴ ![]() 与
与![]() 的夹角
的夹角![]() . ……(8分)
. ……(8分)
17. 解:(1)从袋中10个球中摸出2个,试验的结果共有![]() (种). ……(1分)
(种). ……(1分)
中奖的情况分为两种:
(i)2个球都是红色,包含的基本事件数为![]() ;……(2分)
;……(2分)
(ii)2个球都是白色,包含的基本事件数为![]() . ……(3分)
. ……(3分)
所以,中奖这个事件包含的基本事件数为15+6=21. 因此,中奖概率为![]() .……(4分)
.……(4分)
(2)设两人到达的时间分别为9点到10点之间的x分钟、y分钟.
 用
用![]() 表示每次试验的结果,则所有可能结果为
表示每次试验的结果,则所有可能结果为
![]() ; ……(5分)
; ……(5分)
记甲比乙提前到达为事件A,则事件A的可能结果为
![]() . ……(6分)
. ……(6分)
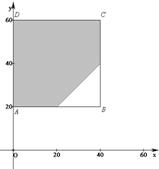
如图所示,试验全部结果构成区域Ω为正方形ABCD. 而事件A所构成区域是正方形内的阴影部分. ……(7分)
根据几何概型公式,得到
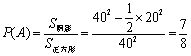 .
.
所以,甲比乙提前到达的概率为![]() . ……(8分)
. ……(8分)
18. 解:(1)函数![]() 的周期
的周期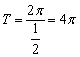
由![]() ,解得
,解得![]() . 列表如下:
. 列表如下:
| x |
|
|
|
|
|
|
| 0 |
| π |
| 2π |
| 3sin( | 0 | 3 | 0 | –3 | 0 |
……(3分)
描出五个关键点并光滑连线,得到一个周期的简图. 图象如下.
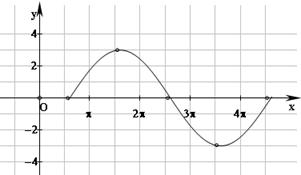 ……(4分)
……(4分)
(2)方法一:先把![]() 的图象向右平移
的图象向右平移![]() 个单位,然后把所有点的横坐标扩大为原来的2倍,再把所有点的纵坐标扩大为原来的3倍,得到
个单位,然后把所有点的横坐标扩大为原来的2倍,再把所有点的纵坐标扩大为原来的3倍,得到![]() 的图象.
……(7分)
的图象.
……(7分)
方法二:先把![]() 的图象所有点的纵坐标扩大为原来的3倍,然后把所有点的横坐标扩大为原来的2倍,再把图象向右平移
的图象所有点的纵坐标扩大为原来的3倍,然后把所有点的横坐标扩大为原来的2倍,再把图象向右平移![]() 个单位,得到
个单位,得到![]() 的图象. ……(7分)
的图象. ……(7分)
(3)方法一:![]() 的周期为
的周期为![]() . ……(8分)
. ……(8分)
解不等式 ![]() ,……(9分)
,……(9分)
得 ![]()
所以,函数![]() 的单调递减区间为
的单调递减区间为![]() . ……(10分)
. ……(10分)
方法二:作出![]() 的图象,由图可知,
的图象,由图可知,![]() 的周期为
的周期为![]() . ……(8分)
. ……(8分)
单调递减区间为![]() . ……(10分)
. ……(10分)
19. 解:(1)散点图如图所示
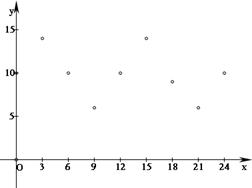 ……(2分)
……(2分)
(2)由散点图可知,选择![]() 函数模型较为合适. ……(3分)
函数模型较为合适. ……(3分)
由图可知,![]() ,T=12,
,T=12,![]() .
.
则![]() ,
,![]() . ……(5分)
. ……(5分)
把t=0代入,得![]() ,即
,即![]() . ……(6分)
. ……(6分)
所以![]() (0≤t≤24). ……(7分)
(0≤t≤24). ……(7分)
(3)由![]() (0≤t≤24),即
(0≤t≤24),即![]() . ……(8分)
. ……(8分)
则![]() ,得
,得![]() ……(9分)
……(9分)
从而 ![]() 或
或![]() 或
或![]() .
.
所以,应在白天11时~19时进行训练. ……(10分)