高一数学科第二学期期末统一考试
数学科试卷
本试卷分第I卷（选择题）、第II卷（非选择题）两部分。共100分，考试时间100分钟。
第I卷（选择题共40分）
注意事项：
1、答第I卷前，考生务必将自己的姓名、统考考号、座位号、考试科目用铅笔涂写在答题卡上。
2、每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试题上。
3、可以使用科学计算器。
4、考试结束，将答题卡交回，试卷不用上交。
一、选择题（每小题4分，共40分）
1. 
= (
)
A. 
B.
C.
D.
2. 在算法中，下列语句正确的是 ( )
A. 
B.
A=A+1 C.
8=x D.
3. 把89化为五进制数，则此数为 ( )
A. 322(5) B. 323(5) C. 324(5) D. 325(5)
4. 下列命题正确的是 ( )
A.
B.
C. 
D.
5. 
(
)
A. 
B.
C.
D.
6. 一个单位有职工160人，其中有业务员104人，管理人员32人，后勤服务人员24人，要从中抽取一个容量为20的样本，用分层抽样的方法抽取样本，则在20人的样本中应抽取管理人员人数为 ( )
A. 3 B. 4 C. 5 D. 6
7. 函数
是 ( )
A. 周期为
的奇函数 B.
周期为的偶函数
C. 周期为
的奇函数 D.
周期为的偶函数
8. 如果事件A与事件B为互斥事件，记A的对立事件为
，B的对立事件为
，则 ( )
A. A与B为对立事件 B.
与一定互斥
C. 与一定不互斥 D.
与不一定互斥
9. 以下有四种说法:
①正切函数在其定义域内是增函数
②
③生产过程中的质量控制图的主要依据是小概率事件在一次实验中几乎不可能发生原理
④由变量x和y的数据得到其回归直线方程
，则l 一定经过点
.
以上四种说法，正确的有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
10. 在区间
上任取三点，则它们到原点O的距离平方和小于1的概率为 ( )
A. 
B.
C.
D.
|
数学科试卷
第II卷（非选择题共60分）
| 题 号 | 二 | 15 | 16 | 17 | 18 | 19 | 总分 | 总分人 | 复分人 |
二、填空题（每小题4分，共16分）
11. 已知
，若
，则实数k的值为
12. 若
，则
13. 计算：cos15°+sin15°= .
14. 若数据
的平均数
=5，方差
，则数据
的方差为
三、解答题（共5小题. 15题8分，16、17、18、19题各9分，合计44分）
|
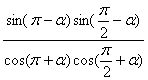（4分）
（2）若
，求
之值（4分）
|
16.设
，求
及
、
间的夹角
（精确到1°）
|
17.已知函数
。
（1）求函数y的最大值及y取最大值时x的集合；
（2）求函数y的单调递减区间；
（3）将函数
的图象作怎样的变换可得到
的图象？
|
18. （1）有4个人，每个人都等可能地被分配到8个房间中的任意一间去住（每个房间可住任意个人），求下列两个事件的概率（结果用分数表示）。
① 编号为1，2，3，4的4个房间各有一个人住；
② 恰好有4个房间，其中各住一个人；
（2）某班级有50人，则至少有两个人的生日在同一天的概率为多大？（一年以365天计，只需列出式子，无需计算出结果）。
|
，且
，求：
（1）及
；
（2）若
的最小值为
，求实数
的值。
第二学期期末统一考试
数学科试卷参考答案
一、CBCDA BBDBC
二、11. 1 12.
13.
14.
18
三、
15．（1）解：原式=
（2）解：原式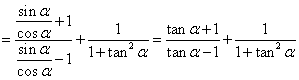
……（3分）
……（4分）
16．解：
……（3分）
又
……（4分）
……（5分）
……（7分）
由计算器，得
……（8分）
……（9分）
17．解：（1）当
时，y取最大值
，此时……（1分）
即
……（2分）
取最大值1时，x的集合为
……（3分）
（2）令
，则
……（4分）
的单调递减区间为
由
得……（5分）
……（6分）
又在
上为增函数，故原函数的单调递减区间为：
……（7分）
（3）法一：将的图象的横坐标变为原来的，再将所得图象向右平移
个单位。……（9分）
法二：将的图象向右平移
个单位，再将所得图象的横坐标变为原来的。……（9分）
18．解：（1）①设A={编号为1，2，3，4的4个房间各有一个人住}，则
则
……（2分）
……（3分）
②设B={恰好有4个房间，其中各住1人}
则
(或
……（5分）
……（6分）
（2）设C={至少有两个人的生日在同一天}
则P(C)=1—P{每个人的生日均不相同}……（7分）
（或
……（9分）
19．解：（1）
……（1分）
……（2分）
又
从而
……（3分）
（2）
……（4分）
由于 故
……（5分）
①当
时，当且仅当
时，
取得最小值
，这与题设矛盾…（6分）
②当
时，当且仅当
时，取得最小值
，由
及得
……（7分）
③当
时，当且仅当
时，取得最小值
，由
，得
与矛盾……（8分）
综上所述，即为所求。……（9分）