高一数学期末复习
一、选择题（每题5分）
1、下列各条件中，不能确定一个集合的一组对象是 （ ）
A、充分接近
的所有实数的全体 B、某校身高不超过1.7米的所有学生
C、小于100的所有偶数 D、数轴上到原点的距离不超过一个单位的点的全体
2、若
，
，则 （ ）
A、
B、
C、P=Q
D、
3、函数
在[0，1]上的最大值与最小值的和为3，则a= （ ）
A、
B、2
C、4
D、
4、直线
的斜率为k，在y轴上的截距为b，则 （ ）
A、
B、
C、
D、
5、二次函数
的图象与x轴的交点的个数为 （ ）
A、0 B、1 C、2 D、无法确定
6、在下列函数中，定义域是R的是 （ ）
A、
B、
C、
D、
7、已知0<a<1,b<—1，则函数+b的图象不经过
（ ）
A、第一象限 B、第二象限 C、第三象限 D、第四象限
8、线面垂直的条件是 （ ）
A、一直线垂直于平面内的一条直线 B、一直线垂直于平面内的两条平行直线
C、一直线垂直于平面内的无数条直线 D、一直线垂直于平面内的任意一条直线
9、下列正确的是 （ ）
A、 空间四点中有三点共线，则此四点共面 B、三个平面两两相交的三条交线共点
C、平面
和平面
只有一个交点 D、空间两组对边分别相等的四边形是平行四边形
10、若a、b是异面直线，且a//平面，则b与的位置关系是
（ ）
A、b//
B、b与相交
C、b在内 D、不确定
11、下列直线中，与直线
相交的直线是
（ ）
A、
B、
C、 
D、
12、点（3，9）关于直线
对称的点的坐标是
（ ）
A、（—1，—3） B、（17，—9） C、（—1，3） D、（—17，9）
二、填空题（每题4分）
13、经过平面的一条斜线可作 个平面与这个平面垂直
14、函数
在区间[2，+
上是增函数，在区间（—
上是减函数，则m=
15、圆
和
的位置关系为
16、一个正四棱柱的侧面展开后是一张长12cm，宽8cm的矩形铁皮，则这个四棱柱的体积是
三、解答题
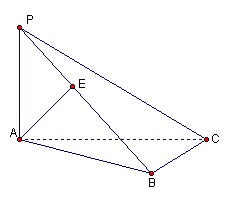
17、三棱锥P—ABC中，PA⊥平面ABC，AB⊥BC，AE⊥PB于E，求证：AE⊥PC（12分）
18、直线过点P（5，6），它在x轴上的截距是在y轴上的截距的2倍，求此直线的方程
（12分）
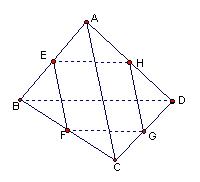
19、如图，在三棱锥A—BCD中，E、F、G、H分别是边AB、BC、CD、DA的中点
（1） 求证：四边形EFGH是平行四边形
（2） 若AC=BD，求证：四边形EFGH为菱形
（3） 当AC与BD满足什么条件时，四边形EFGH为正方形
20、求由下列条件所决定的圆
的切线方程
（1）斜率为—1
（2）过点P（
，1）
21、已知两条直线
：
，
：
，求满足下列条件的m的值
（1）与相交
（2）与平行
（3）与垂直
22、已知ABCD—A1B1C1D1是棱长为a的正方体
（1）求异面直线BC1和AC所成的角
（2）求BC1和平面ABC所成的角
（3）求C1—BD—C的正切值
