高一数学期末考试模拟（1）

高一数学期末考试模拟（1）

一、选择题（每小题3分，共计30分）（以下每个问题的四个选项中，有且只有一个选项是正确的）

1．已知数列3,3,3,3,3. 则该数列为（　　 ）

A．等差数列但不是等比数列　　　　　　　　 B．等比数列但不是等差数列

C．既是等差数列也是等比数列　　　　　　　 D．既不是等差数列也不是等比数列

2．设数列是递增的等差数列，前三项的和为15、积为80，则它的首项为（　 ）

A．1　　　　  B．2　　　　 C．4　　　　D．5

3．等比数列的前n项和为S_n=3ⁿ⁺¹－a，则实数a的值为（　 ）

A．3　　　　　　 B．　　　　  C．－3　　　　  D．－

4．在等比数列中，若前n项和S_n=25，前2n项和S_2n=100，则前3n项和S_3n=（　　）

A．325 　　　　　B． 225　　　　　  C． 200　　　　  D．175

5．设f(n)=1++……+，则必有(　　 )

A．f(1)=1　　　　B．f(1)=1+　　 C．f(1)=1+　　  D．f(1)=1+

6．已知函数f(x)=a^x(a>0且a)，则对于任意的实数x, y 都有(　　 )

A．f(xy)=f(x)f(y )　　 B．f(xy)=f(x)+f(y)　　C．f(x+y)=f(x)f(y )　  D．f(x+y)=f(x)+f(y)

7．某工厂去年12月份的产量是去年1月份产值的m倍，则该厂去年月产值的平均增长率为（　　）

A．　　　　B．　　  C．　　  D．

8．已知f(x⁵)=log₂x，则f(2)的值为（　　　）

A．1　　 　　B．5　　　　 C．－5　　 　　　D．

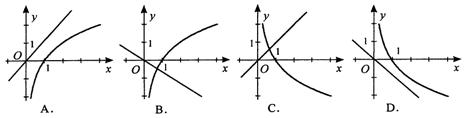9．当a>1时，函数y=log_ax和y=(1－a)x的图象只可能是（　　 ）

10．将函数f(x)的图象C向左平移2个单位得到C₁，再将C₁作关于y轴的对称图形得到C₂，有同学说，实际上只要作一个图形变换就可使C₂变换到C，那么，这变换是（　　）

A．关于直线x=1 对称　　　　B．关于直线x=－1对称

C．关于直线x=2对称　　　　 D．关于直线x=－2对称

二．填空题（每小题4分，共计24分）

11．已知两实数1与x的等差中项为4，若三个数1，y，x成等比数列，则y=______。

12．若一个等差数列的前3项和为34，最后3项的和为146，所有项的和为780，则这个数列的项数为_______________。

13．已知函数f(x)=2^－x，若f^－1(a)=4，则实数a=________________。

14．设函数f(x)=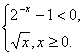若f(x₀)>1，则x₀的取值范围是_____________。

15．已知S_n表示等比数列的前n项和，a₁=1，，则该等比数列的公比q=___

16．使log₂(－x)<x+1成立的x的取值范围是____________。

三．解答题（本大题共计46分，附加题5分另计）

17．（本题8分）

求函数y=　 x的反函数。

18．（本小题8分）

设为等差数列，已知a₃=11,a₈=31.

(1)　　求a_n；

(2)　　若S_n为数列的前n项和，T_n为数列的前n项和，求T_n。

19．（本小题10分）

在等差数列中，a₁=2，a₁+a₂+a₃=12。

(1) 求数列的通项公式；

(2) 令b_n=a_n·3ⁿ，求数列的前n项和S_n

参考答案

一．选择题

1.C　　2.B　　3.A　　4.A　　 5.D　　6.C　　 7.D　　8.D　　9.B　　 10.A　　

二．填空题

11. 　　　　12.　26　　　13.　　　 14.(－1, 1)　　　 15.　 16.(－1,  0)

三．解答题

17.解：∵,　 ∴ 即　∴x=ln

∵x>0 ,　∴e^x>1.　　∴y=1+.(法二：∴ y>1)

∴y=, x的反函数为y=ln.(x>1)

18.解：（1）设数列的公差为d，

则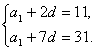　 ∴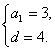　　∴a_n=4n－1

(2)　∵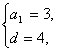　　 ∴S_n=2n²+n

∴ 　

∴

19.解：（1）设数列的公差为d

∵　　∴3　　  ∴　　

∴d=　　  ∴　

(2)∴　　　　 ∴……①

∴………②

①　　 －②得：

=

∴

22．解：s=9+2×9²+3×9³+…+9×9⁹=9+9²+9³+…+9⁹+9(s－9¹⁰)=

∴s=

高一年级（上）期末考试模拟（2）

一、选择题：本大题共 12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．

1、设集合M={xy=logax，a>0且a≠1}，集合N={yy=ax，a>0，且a≠1}，则下列结论中正确的是（ ）

A．MN　　　　　B．M∪N=R　　　　  C．NM　　　　　D．以上都不对

2、已知函数f(x)=ax＋b的图象过点（1，7），其反函数f－1(x)的图象过点（4，0），则f(x)的表达式是（ ）

A．3x＋4　　　　　　B．4x＋3　　　　　　 C．2x＋5　　　　　　D．5x＋2

3、三角形ABC中，∠B=60°是三角形内角A、B、C成等差数列的（ ）

A．充要条件 　　　B．充分不必要条件　　　 C．必要不充分条件 　　　D．既不充分也不必要条件

4、夏季高山上气温从山脚起每升高100米降低0.7℃，已知山顶气温是14.1℃，山脚的气温是26℃，那么此山相对于山脚的高度是（ ）

A．1500米 　　　　B．1600米　　　　  C．1700米　　　　　D．1800米

5、已知函数在（0，＋∞）上是单调减函数，则实数a满足的条件是（ ）

A．a>1　　　 　B．a<2　　　　 C．a<　　　 D．1<a<

6、在等差数列{an}中，a3＋a11=40，则a6＋a7＋a8的值为（ ）

A．48 　　　　　B．60　　　　　 C．72 　　　　 D．84

7、设a>b>0，a＋b=1，令则x、y、z的大小关系为（ ）

A．x>y>z　　　　　B．x>z>y　　　　　 C．z>x>y　　 　　D．z>y>x

8、已知a、b、c成等比数列，则二次函数f(x)=ax2＋bx＋c的图象与x轴交点个数是（ ）

A．0　　　　 　B．1　　　　　　 C．2　　　　　D．0或1

9、{an}为等比数列，若，则S8的值等于（ ）

A．12 　　　　　　B．24　 　　　　　C．16 　　　  　D．32

10、如果f(a＋b)=f(a)·f(b)，且f(1)=2，则等于（ ）

A．2000 　　　　B．2002　　　　　 C．2003 　　　　D．2004

11、已知数列{an}的通项公式，设其前n项和为Sn，则使Sn<－5成立的自然数n（ ）

A．有最小值63 　　　　B．有最大值63　　　　　　 C．有最小值31 　　　　D．有最大值31

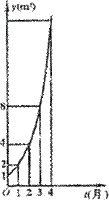12、如图所示的是某池塘中的浮萍蔓延的面积y（m2）与时间t（月）的关系：y=at，有以下叙述：

①这个指数函数的底数为2； ②第5个月时，浮萍面积就会超过30m2；

③浮萍从4m2蔓延到12m2需要经过1.5个月； ④浮萍每月增加的面积都相等；

⑤若浮萍蔓延到2m2、3m2、6m2所经过的时间分别为t1、t2、t3，则t1＋t2=t3.　　　其中正确的是（ ）

A．①②　　　　　 B．①②③④　　　　　  C．②③④⑤　　　　　 D．①②⑤

二、填空题：本大题共 4小题，每小题4分，共16分．

13、lg20＋log10025=___________.

14、若f(x)=2x，则方程f－1(x－1)＋f－1(x)=1的解集为___________.

15、已知命题p：不等式x＋x－1>m的解集为R，命题q：f(x)=－(5－2m)x是减函数，若p或q为真命题，p且q为假命题，则实数m的取值范围是___________.

16、根据市场调查结果，预测某种家用商品从年初的12个月内累计的需求量Sn（万件）近似地满足，按此预测，在本年度内需求量超过1.5万件的月份是___________.

三、解答题

18、（本小题满分12分）已知数列{an}是等差数列，其中a1=1，S10=100，求通项an；又对上述的{an}，设an=log2bn，试求数列{bn}的前5项的和T5.

19、（本小题满分12分）已知函数.

（1）求f(x)的定义域； （2）求f(x)的值域； （3）求f(x)的单调递减区间.

20、（本小题满分12分）设0<a<1，函数，设f(x)和g(x)的定义域的公共部分为D，当[m，n]D时，f(x)在[m，n]（m<n）上的值域是[g(n)，g(m)]，求a的取值范围.

21、（本小题满分14分）已知数列{an}是首项a1>1，公比q>0的等比数列，设bn=log2an（n∈N*），且b1＋b3＋b5=6，b1b3b5=0.

（1）求数列{an}的通项公式；　　 （2）设数列{bn}的前n项和为Sn，求证：数列是等差数列；

（3）设数列的前n项和为Tn，当Tn取最大值时，求n的值.

答案：一、1、C,　　2、B提示：由题意知点（1，7）和（0，4）在函数f(x)的图象上，

　　　∴ .

3、A　　 提示：B=60° A＋C=120°2B=A＋C，　　　A＋C=2B 3B=180°B=60°.

4、C　 提示：， 　　　∴ 所求 =100×17=1700（米）.

5、D　　提示：依题意知，

6、B　　　7、B提示：依题意 0<b<a<1，故.

　　　故 ，　　　即 x>z>y.

8、A　　提示：由已知 b²=ac>0，又△=b²－4ac=b²－4b²=－3b²<0.

9、A　 提示：依题意知.

10、D　　 提示：，∴ ，原式=

11、A　　 提示：

　　　由

12、D　　　　  提示：由图象可知①②⑤正确 .

二、13、2　　　提示：原式 = .

14、{2}　　 提示：设 y=f(x)，则y=2^x，得x=log₂y，∴ f^－1(x)=log₂x，

　　　∴ 方程即是 log₂(x－1)＋log₂x=1，即log₂[x(x－1)]=1， 　　　∴ x²－x=2，解得x=2或x=－1（舍去）.

15、[1，2）　　提示：由 x＋x－1＞m的解集为R，则m＜1，

　　　由－(5－2m)^x为减函数，则m<2，　　　又由 p或q为真，p且q为假，∴ 1≤m<2.

16、7或8　　 提示：设每月的需求量为 a_n，则 　　　 .

　　　且 ， 　　　∴ 6<n<9，∴ n∈N_＋，∴ n=7或8.

三18、解：由 a₁=1，S₁₀=100，得100=10＋45d，故d=2.

　　　而，∴ 数列{b_n}是首项为2，公比为4的等比数列，

　　∴ {b_n}的前5项的和

19、解：（1）由－x²＋2x＋3>0得函数f(x)的定义域为{x－1<x<3}.

　　（2）令t=－x²＋2x＋3=－(x－1)²＋4 (－1<x<3). 　　　　 ∴ t的值域是（0，4].

　　　　 又是减函数， 　　　　 ∴ f(x)的值域是[－2，＋∞）.

　　（3）∵ t=－(x－1)²＋4（－1<x<3）的递增区间是（－1，1]， 　　　　 ∴ f(x)的单调递减区间是(－1，1].

20、解：由 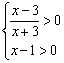得 x>3，∴ D={xx>3}.

由 [m，n] D，∴ n>m>3，又0<a<1，∴ f(x)在[m，n]上为减函数.

　　∴ 则m，n是f(x)=g(x)比3大的两个不等正根， 即为 ，整理得 ax²＋(2a－1)x＋3－3a=0（x>3）. 　　令

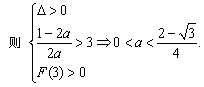
21、解：（1）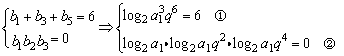

　　　　　由①得 a₁q²=4 　　　　　　　　　　③ 　　　　　∵ a₁>1，则由②得 a₁q⁴=1　　　　　④

　　　　　④÷③得.

　　（2）∵

　　　　　故是首项为4，公差为－的等差数列.

　　（3）∵ n≤8时，，n=9时，=0，n≥10时，<0.

　　　　　故当 n=8或9时，T_n最大．