高 一 数 学 期 考 模 拟 题（1）
班级： 姓名：
一、选择题（每小题3分，共45分，请将所选答案填在括号内）
1. 下列关系中正确的个数为
①0∈{0}，②Φ
{0}，③{0，1}
{（0，1）}，④{（a，b）}＝{（b，a）} (
)
A. 1 B. 2 C. 3 D. 4
2．已知集合A={0，4}，B={0，2}，下列从A到B的对应关系为f，x∈A，y∈B，不是映射的是 （ ）
A、
B、
C、
D、
3. 直线y=3与函数y=x2-6x 图象的交点个数为 ( )
A. 4个 B. 3个 C. 2个 D. 1个
4．已知a,b,c成等比数列，且x,y分别为a与b、b与c的等差中项，则
的值为（ ）
A.
B.-2
C.2
D. 不确定
5．某种细菌在培养过程中，每20分钟分裂一次(一个分裂为两个)，经过3小时，这种细菌由1个可繁殖成 （ ）
A．511个 B．512个 C．1023个 D．1024个
6．
2的必要非充分条件是 （ ）
A．
B．
C．
D．
7．等差数列{
}中，已知
（ ）
A．48 B．49 C．50 D．51
8．已知
的反函数
－1(x)的图像的对称中心是(—1，3)，则实数a等于
A．2 B．3 C．－2 D．－4
9．已知
，其中
，则下列不等式成立的是 （ ）
A．
B．
C．
D．
10．函数f(x)=
＋2 (x≥1)的反函数是
（
）
A．y=(x－2)2＋1 (x∈R) B．x=(y－2)2＋1 (x∈R)
C．y=(x－2)2＋1 (x≥2) D．y=(x－2)2＋1 (x≥1)
11．已知不等式
的解集为空集，则实数
的取值范围为
（ ）
A．
B．
C．
D．
12．等比数列｛an｝的首项a1＝1，公比q≠1，如果
依次是某等差数列的第1，2，5项，则q等于
（
）
A．2 B．3 C．－3 D．3或－3
13．满足
的集合B的个数是
（ ）
A．1 B．2 C．3 D．4
14. 若
，
，
成等差数列，则
的值为
（ ）
A、 B、
C、
D、或-log32
15．若函数
在区间
是减函数，则
的取值范围是（ ）
A、
B、
C、
D、
二、填空题（每小题3分，共15分，请将答案填在横线上）
16．函数
[
]图象与其反函数图象的交点坐标为 ．
17．若
且
，则的取值范围是 ．
18．若
恒成立，则实数的取值范围是__________________．
19. 已知等差数列{}，以（n，）为坐标的点均在直线y=2kx－(k－12)上，并从
开始各项均小于零，则d的取值范围
20．已知等比数列
及等差数列
，其中
，公差d≠0．将这两个数列的对应项相加，得一新数列1，1，2，…，则这个新数列的前10项之和为_________________.
三、解答题（本大题每小题8分，共40分）
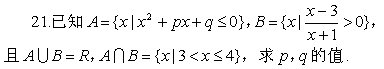
22．若函数y=
的定义域为R，求实数k的取值范围。
23．数列｛｝满足
（1）若
，求证｛
｝为等比数列；（2）求｛｝的通项公式．
24．设函数f(x)是定义在R+上的增函数，且f(xy)= f(x)+ f(y)（x、y∈R+），f(2)=1
(1)求f(1)
(2)求满足f(x)+ f(x-3)≤2的x的取值范围
25. 某公司实行股份制，一投资人年初入股a万元，年利率为 25%，由于某种需要，从第二年起此投资人每年年初要从公司取出x万元.
（1）分别写出第一年年底，第二年年底，第三年年底此投资人在该公司中的资产本利和；
（2）写出第n年年底此投资人的本利之和bn与n的关系式（不必证明）；
（3）为实现第20年年底此投资人的本利和对于原始投资a万元恰好翻两番的目标，若a=395，则x的值应为多少？（在计算中可使用lg2=0.3）
参考答案
一．B B A C B A C A C C B B D A B
二．16.
， 17.
， 
19．
20. 978
三． 21. 
由根与系数的关系得：
22．由f(－1)=－2得：1－(2＋lga)＋lgb=－2 即lgb=lga－1 ① 
由f(x)≥2x恒成立，即x2＋(lga)x＋lgb≥0， ∴lg2a－4lgb≤0，
把①代入得，lg2a－4lga＋4≤0，(lga－2)2≤0
∴lga=2，∴a=100，b=10
23. (1)设x=y=1，则f(1)=f(1)+f(1) ∴ f(1)=0
(2) ∵f(x)+ f(x-3)≤2
∴f[x(x-3)]≤f(4) 又 f(x)为增函数 ∴ x(x-3)≤4
∴
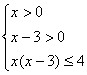即3＜x≤4
24． (1)由an=
an－1＋1得an－2= (an－1－2)
即
，(n≥2)
∴｛bn｝为以－1为首项，公比为的等比数列
(2)bn=(－1)( )n－1，即an－2=－()n－1
∴an=2－()n－1
25.（1）第一年年底本利和：a+a·25%=1.25a
第二年年底本利和：(1.25a－x)+(1.25a－x)25%=1.252a－1.25x
第三年年底本利和：（1.252a－1.25x－x）+（1.252a－1.25x－x）25%
=1.253a－（1.252a+1.25）x
（2）第n年年底本利和：bn=1.25na－(1.25n－1+1.25n－2+…+1.25)x
（3）依题意有：
395×1.2520－(1.2519+1.2518+…1.25)x=4×395
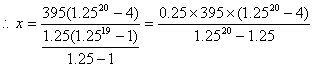①
设1.2520=t ∴lgt=201g(
)=20(1－31g2)=2
∴t=100代入①解得x=96