高中数学新课标必修③④综合测试卷
命题人:高建彪 时量:100分钟 满分:100分
一、选择题(每小题4分,共10小题,共40分)
1. 已知向量![]() =(4,2),向量
=(4,2),向量![]() =(
=(![]() ,3),且
,3),且![]() //
//![]() , 则
, 则![]() 等于
等于
A. 9 B. 6 C. 5 D. 3
2. tan600°的值是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3. 某地区有300家商店,其中大型商店有30家,中型商店有75家,小型商店有195家. 为了掌握各商店的营业情况,要从中抽取一个容量为20的样本. 若采用分层抽样的方法,抽取的中型商店数是
A. 2 B. 3 C. 5 D. 13
4. 下列各数中最小的数是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
5. 为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5岁-18岁的男生体重(kg) ,得到频率分布直方图如下:
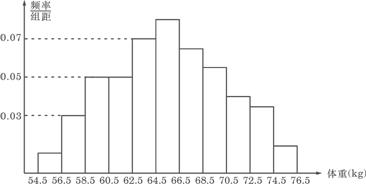
根据上图可得这100名学生中体重在〔56.5,64.5〕的学生人数是
A. 20 B. 30 C. 40 D. 50
 6. 已知向量
6. 已知向量![]() 与
与![]() 的夹角为
的夹角为![]() ,
,![]() 则
则![]() 等于
等于
A. 5 B. 4 C. 3 D. 1
7. 若△![]() 的内角
的内角![]() 满足
满足![]() ,则
,则![]() =
=
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
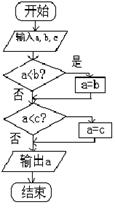
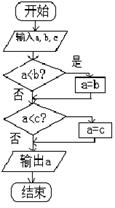
8. 右图给出一个算法的程序框图,该程序框图的功能是
A.求输出a,b,c三数的最大数 B.求输出a,b,c三数的最小数
C.将a,b,c按从小到大排列 D.将a,b,c按从大到小排列
9. 已知![]() 则
则![]() 等于
等于
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
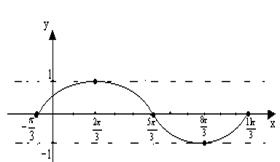
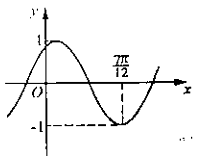 10. 将函数
10. 将函数![]() 的图象沿x轴方向左平移
的图象沿x轴方向左平移![]() 个单位,平移后的图象如右图所示. 则平移后的图象所对应函数的解析式是
个单位,平移后的图象如右图所示. 则平移后的图象所对应函数的解析式是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
▲请将选择题答案对应填写在下表中:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、填空题(每小题4分,共4小题,共16分)
11. ![]() 的值为
.
的值为
.
12. 已知向量![]() ,
,![]() ,则
,则![]() 的最大值为 .
的最大值为 .
13. 某班委会由4名男生与3名女生组成,现从中选出2人担任正副班长,其中至少有1名女生当选的概率是 . (用分数作答)
14. 规定运算![]() ,若
,若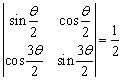 ,则
,则![]() = .
= .
三、解答题(共5个题. 15题8分、16、17、18、19题各9分,合计44分)
15. 已知![]() ,
,![]() ,
,
(1)求![]() 与
与![]() 的夹角
的夹角![]() ;
;
(2)若![]() ,且
,且![]() ,试求
,试求![]() .
.
 16. (1)有10本不同的语文书,2本不同的数学书,现从中任意取出2本,能取到数学书的概率有多大?
16. (1)有10本不同的语文书,2本不同的数学书,现从中任意取出2本,能取到数学书的概率有多大?
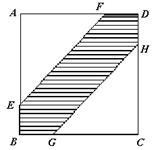
(2)如图,在边长为25cm的正方形ABCD中挖去边长为23cm的两个等腰直角三角形,现有均匀的粒子散落在正方形中,问粒子落在中间带形区域的概率是多少?
17. 已知函数![]() .
.
(1)用五点法画出它在一个周期内的闭区间上的图象;
(2)说明此函数图象可由![]() 上的图象经怎样的变换得到;
上的图象经怎样的变换得到;
(3)由图象指出函数的单调递减区间、对称轴方程和对称中心点坐标.
18.设向量![]() =(sinx,cosx),
=(sinx,cosx),![]() =(cosx,cosx),x∈R,函数f(x)=
=(cosx,cosx),x∈R,函数f(x)=![]() .
.
(1)求函数f(x)的最大值与最小正周期;
(2)求使不等式f(x)≥![]() 成立的x的取值集合.
成立的x的取值集合.
19. 下表是芝加哥1951~1981年月平均气温(华氏):
| 月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 平均气温 | 21.0 | 26.0 | 36.0 | 48.8 | 59.1 | 68.6 | 73.0 | 71.9 | 64.7 | 53.5 | 39.8 | 27.7 |
(1)以月份为x轴,x=月份-1,以平均气温为y轴,描出散点图,并用一个函数模型近似地描述y与x之间的函数关系.
(2)某蔬菜的种植,要求每月的平均气温不低于60华氏,试确定蔬菜在一年内种植的最长时间.
高中数学新课标必修③④综合测试卷
时量:100分钟 满分:100分
一、选择题(每小题4分,共10小题,共40分)
1. 已知向量![]() =(4,2),向量
=(4,2),向量![]() =(
=(![]() ,3),且
,3),且![]() //
//![]() , 则
, 则![]() =( ).
=( ).
A. 9 B. 6 C. 5 D. 3
答案:B
简解:(06年全国卷Ⅱ.文1)由![]() ,解得
,解得![]()
2. tan600°的值是( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
答案: D
简解:(2005年湖南卷.文2)![]() ,故选D
,故选D
3. 某地区有300家商店,其中大型商店有30家,中型商店有75家,小型商店有195家. 为了掌握各商店的营业情况,要从中抽取一个容量为20的样本. 若采用分层抽样的方法,抽取的中型商店数是( ).
A. 2 B. 3 C. 5 D. 13
答案: C
简解:(2006年重庆卷.文7)![]()
4. 下列各数中最小的数是( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
答案:D
简解:都化为十进制,![]() ;
;![]() ;
;![]() ;
;![]()
5. 为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5岁-18岁的男生体重(kg) ,得到频率分布直方图如下:

根据上图可得这100名学生中体重在〔56.5,64.5〕的学生人数是( ).
A. 20 B. 30 C. 40 D. 50
答案:C
简解:(2006年重庆卷.理6)由图可知,在〔56.5,64.5〕的频率为
![]() ,则学生人数为
,则学生人数为![]()
6. 已知向量![]() 与
与![]() 的夹角为
的夹角为![]() ,
,![]() 则
则![]() 等于(
).
等于(
).
A. 5 B. 4 C. 3 D. 1
答案:B
简解:(06年福建卷.文9)![]()
=![]() .
.
即![]() ,解得
,解得![]() (
(![]() 舍). 所以选B.
舍). 所以选B.
7. 若△![]() 的内角
的内角![]() 满足
满足![]() ,则
,则![]() =(
).
=(
).
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
答案: A
简解:(2006年湖北卷)∵![]() ,∴
,∴![]() .
.
∴![]() ,
,![]() =
=![]()
![]()
![]() .
.
8. 右图给出一个算法的程序框图,该程序框图的功能是( ).
A.求输出a,b,c三数的最大数 B.求输出a,b,c三数的最小数
C.将a,b,c按从小到大排列 D.将a,b,c按从大到小排列
答案:A
简解:略
9. 已知![]() 则
则![]() 等于(
).
等于(
).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
答案:A
 简解: (2006年福建卷)由
简解: (2006年福建卷)由![]() ,得
,得![]() ,
,![]() .
.
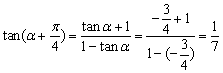
10. 将函数![]() 的图象沿x轴方向左平移
的图象沿x轴方向左平移![]() 个单位,平移后的图象如右图所示. 则平移后的图象所对应函数的解析式是( ).
个单位,平移后的图象如右图所示. 则平移后的图象所对应函数的解析式是( ).
A.![]() B.
B.![]()
C.![]() D.
D.![]()
答案:C
简解:(2006年安徽卷改编)将函数![]() 的图象向左平移
的图象向左平移![]() ,平移后的图象所对应的解析式为
,平移后的图象所对应的解析式为![]() ,由图象知,
,由图象知,![]() ,所以
,所以![]() ,因此选C.
,因此选C.
或者设平移后图象的解析式为![]() ,由图可知
,由图可知![]() ,
,![]() ,则
,则![]() . 当
. 当![]() 时,
时,![]() ,解得
,解得![]() . 选C.
. 选C.
二、填空题(每小题4分,共4小题,共16分)
11. ![]() 的值为
.
的值为
.
答案:-![]()
简解:(2006年陕西卷)原式=![]()
12. 已知向量![]() ,
,![]() ,则
,则![]() 的最大值为 .
的最大值为 .
答案:![]()
简解:(06年江西卷.文13)![]() =sinq-cosq=
=sinq-cosq=
![]() £
£![]()
13. 某班委会由4名男生与3名女生组成,现从中选出2人担任正副班长,其中至少有1名女生当选的概率是 . (用分数作答)
答案:![]()
简解:(04年广东卷.13)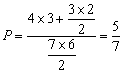
14. 规定运算![]() ,若
,若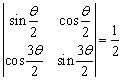 ,则
,则![]() = .
= .
答案:![]()
简解: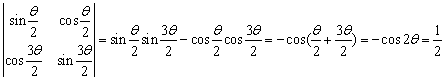 ,则
,则
![]() ,又
,又![]() ,则
,则![]() .
.
三、解答题(共5个题. 15题8分、16、17、18、19题各9分,合计44分)
15. 已知![]() ,
,![]() ,
,
(1)求![]() 与
与![]() 的夹角
的夹角![]() ;
;
(2)若![]() ,且
,且![]() ,试求
,试求![]() .
.
解:(1)∵![]() =61,
=61,
∴ ![]() =
=![]() ,
,
∴ ![]() .
.
(2)设![]() ,则
,则
![]() ,解得
,解得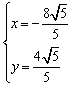 或
或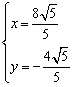 .
.
所以,![]() 或
或![]() .
.
 16. (1)有10本不同的语文书,2本不同的数学书,现从中任意取出2本,能取到数学书的概率有多大?
16. (1)有10本不同的语文书,2本不同的数学书,现从中任意取出2本,能取到数学书的概率有多大?
(2)如图,在边长为25cm的正方形ABCD中挖去边长为23cm的两个等腰直角三角形,现有均匀的粒子散落在正方形中,问粒子落在中间带形区域的概率是多少?
解:(1)基本事件的总数为:12×11÷2=66,
“能取到数学书”这个事件所包含的基本事件个数分两种情况:
(i)“恰好取出1本数学书”所包含的基本事件个数为:10×2=20
(ii)“取出2本都是数学书”所包含的基本事件个数为:1
所以“能取到数学书”这个事件所包含的基本事件个数为:20+1=21
因此, P(“能取到数学书”)=![]()
(2)因为均匀的粒子落在正方形内任何一点是等可能的,所以符合几何概型的条件.
设A=“粒子落在中间带形区域”则依题意得:
正方形面积为:25×25=625,
两个等腰直角三角形的面积为:2×![]() ×23×23=529,
×23×23=529,
带形区域的面积为:625-529=96.
∴ P(A)=![]() .
.
17. 已知函数![]() .
.
(1)用五点法画出它在一个周期内的闭区间上的图象;
(2)说明此函数图象可由![]() 上的图象经怎样的变换得到;
上的图象经怎样的变换得到;
(3)由图象指出函数的单调递减区间、对称轴方程和对称中心点坐标.
解:(1)![]() .
.
 最小正周期
最小正周期 ![]()
先列表,后描点并画图
|
| 0 |
| π |
| 2π |
| x |
|
|
|
|
|
| y | 0 | 1 | 0 | -1 | 0 |
(2)把y=sinx的图象上所有的点向左平移![]() 个单位长度,得到
个单位长度,得到![]() 的图象,再把所得图象的横坐标伸长到原来的2倍(纵坐标不变),得到
的图象,再把所得图象的横坐标伸长到原来的2倍(纵坐标不变),得到![]() 的图象.
的图象.
或把y=sinx的图象横坐标伸长到原来的2倍(纵坐标不变),得到![]() 的图象. 再把所得图象上所有的点向左平移
的图象. 再把所得图象上所有的点向左平移![]() 个单位长度,得到
个单位长度,得到![]() ,即
,即![]() 的图象.
的图象.
(3)单调递减区间为![]() ;
;
对称轴方程为![]() ;对称中心点坐标为
;对称中心点坐标为![]() .
.
18.设向量![]() =(sinx,cosx),
=(sinx,cosx),![]() =(cosx,cosx),x∈R,函数f(x)=
=(cosx,cosx),x∈R,函数f(x)=![]() .
.
(1)求函数f(x)的最大值与最小正周期;
(2)求使不等式f(x)≥![]() 成立的x的取值集合.
成立的x的取值集合.
解:(06年湖北卷.文16)
(1)![]()
![]()
∴![]() 的最大值为
的最大值为![]() ,最小正周期是
,最小正周期是![]() .
.
(2)由(1)知
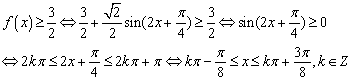
即![]() 成立的
成立的![]() 的取值集合是
的取值集合是![]() .
.
19. 下表是芝加哥1951~1981年月平均气温(华氏):
| 月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 平均气温 | 21.0 | 26.0 | 36.0 | 48.8 | 59.1 | 68.6 | 73.0 | 71.9 | 64.7 | 53.5 | 39.8 | 27.7 |
(1)以月份为x轴,x=月份-1,以平均气温为y轴,描出散点图,并用一个函数模型近似地描述y与x之间的函数关系.
(2)某蔬菜的种植,要求每月的平均气温不低于60华氏,试确定蔬菜在一年内种植的最长时间.
解:(1)作出的散点图如图所示. 根据图形,可选择正弦曲线![]() 进行拟合.
进行拟合.
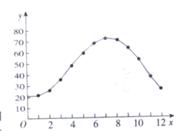 易知,
易知,![]() ,T=12,
,T=12,![]() .
.
则![]() ,
,![]()
把x=0代入,得![]() ,即
,即![]() .
.
所以,拟合的函数模型为![]() .
.
(2)由![]() ,即
,即![]() ,解得
,解得![]() .
.
所以,该蔬菜在一年内种植的最长时间为5个月.