高一数学必修④基础题型归类

高中新课标数学必修④模块 基础题型归类

1、运用诱导公式化简与求值：

要求：掌握,,,,,等诱导公式. 记忆口诀：奇变偶不变，符号看象限.

例1. （1）求值：；　（2）化简： cos²(－α)+cos²(+α)

练1 （1）若cos(π+α)=，<α<2π, 则sin(2π－α)等于　　　　 .

（2）若，那么的值为　　　 .

（3）sin(π)的值为　　　 .

2、运用同角关系化简与求值：

要求：掌握同角二式（,），并能灵活运用. 方法：平方法、切弦互化.

例2 （1）化简；　　（2）已知sinx+cosx=, 且0<x<π, 求tanx的值.

练2 （1）已知sinα·cosα＝，且＜α＜，则cosα－sinα的值为　　　　　　 .

（2）已知tanα=3, 计算：（i）； （ii）sin²α-3sinαcosα+4cos²α.

3、运用和差角、倍角公式化简与求值：

要求：掌握和差角公式、倍角公式，能够顺用、逆用、活用，掌握基本方法（平方、1的妙用、变角、切弦互化、方程思想）.

例3 （1）已知tan（+α）=2，求sin2α+sin²α+cos2α的值.

（2）已知，求的值

练3 （1）若sin（－α）＝，则cos2α＝　　　 .

（2）已知 且则=　　　　　　  .

（3）如果，那么=　　　　　　 .

（4）如果，那么sin⁴x＋cos⁴x=　　　　　  .

（5）△ABC中，已知sinA=, cosB=, 则sin(A+B)的值为　　　　　  .

（6）已知α,β∈（0,π）且，则的值为　　　　 .

（7）已知，则的值为　　　　  .

（8）已知sin（α+β）=，sin（α－β）=，求的值.

4、结合三角变换研究三角函数性质：

要求：熟练进行三角变换，将化为一个三角函数后研究性质. 方法：降次、化一、整体.

例4 已知函数.

（i）求的最小正周期及取得最小值时x的集合；

（ii）在平面直角坐标系中画出函数在一个周期内的图象；

（iii）说明的图象如何由变换得到；

（iv）求的单调区间、对称轴方程.

练4 （1）若函数y=2sinx＋cosx＋4的最小值为1，则a=　 　　　.

（2）函数的最小正周期为　　　　 ；函数的最大值是　　  .

（3）已知函数. 求的最小正周期、单调区间、图象的对称轴，对称中心.

5、运用单位圆及三角函数线：

要求：掌握三角函数线，利用它解简单的三角方程与三角不等式. 方法：数形结合.

例5 （1）已知，则、、的大小顺序为　　　　　　　 .

（2）函数的定义域为　　　　　　  .

练5 （1）若, 则角α的取值集合为____________.

（2）在区间（0，2）内，使sinx<cosx成立的x的取值范围 　　　　.

6、弧度制与扇形弧长、面积公式：

要求：掌握扇形的弧长与面积计算公式，掌握弧度制. 方法：方程思想.

例6 某扇形的面积为1，它的周长为4，那么该扇形圆心角的弧度数为　　　　  .

练6 （1）终边在直线上的所有角的集合为　　　　　　  ，其中在－2π～2π间的角有　　  .

（2）若α为第三象限角，那么－α，、2α为第几象限的角?

7、三角函数的定义、定义域与值域：

要求：掌握三角函数定义（单位圆、终边上点），能求定义域与值域. 方法：定义法、数形结合、整体.

例7 （1）角α的终边过点P（－8m，－6cos60°）且cosα=－，则m的值是　　　　.

（2）当时，函数的值域为　　　 .

练7 （1）函数的定义域为____________.

（2）函数的值域为　　　　　　　   .

（3）把函数y＝sin(2x＋)的图像上各点的横坐标变为原来的，再把所得图像向右平移，得到　　 .

8、 三角函数的图象与性质：

要求：掌握五点法作图、给图求式，由图象研究性质. 方法：五点法、待定系数法、数形结合、整体.

例8 （1）已知函数.求的最小正周期、定义域、单调区间.

（2）已知函数. （i）求此函数的周期，用“五点法”作出其在长度为一个周期的闭区间上的简图. （ii）求此函数的最小值及取最小值时相应的x值的集合

练8 （1）函数最高点D的坐标是，由最高点运动到相邻的最低点时，函数图象与x轴的交点坐标是(4，0)，则函数的表达式是　　　　  .

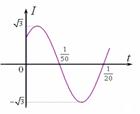
（2）如图，它表示电流在一个周期内的图象. 则其解析式为　　　　　  .

（3）函数的单调减区间为　　　　　　　  .

（4）函数的图象和直线y=2所围成的封闭图形的面积为　　　　　　  .

（5）画出函数，x∈R的简图. 并有图象研究单调区间、对称轴、对称中心.

9、向量基本运算（加减法、数乘、数量积、坐标运算）：

要求：掌握向量加减法几何意义，能熟练进行向量运算，运用向量的运算研究向量平行与垂直.

例9 （1）已知的夹角为120°，且，，当时，k=　　　.

（2）若=（1，2），=（，2）， k为何值时:（i）k+与－3垂直；（2）k+与－3平行？

练9 （1）若，，则的数量积为　　  .

（2）向量与共线且方向相同，则=　　　　　　.

（3）已知A（3，y），B（，2），C（6，）三点共线，则y=_________.

（4）已知  =(－3，4)，若＝1，⊥，则= 　　　　 .

10、向量的模与夹角：

要求：能运用向量运算研究向量的模与夹角问题.

例10 （1）已知=4，=3，（2－3）·（2+）=61，求：(i)与的夹角θ; (ii) .

（2）已知的顶点坐标分别为A（1,2），B（2,3），C（－2,5），求.

练10 （1）非零向量和满足：，则与的夹角等于　　　　 .

（2）已知=10，=12，且（3）·（）=－36，则与的夹角是　　　 .

（3）如果＝1，＝2，与的夹角为，则等于　　　　 .

11、向量与三角函数的交汇考查：

要求：掌握向量与三角函数的交汇. 向量坐标运算是交汇点.

例11 （1）设=（sinx－1，cosx－1），=（，）. （i）若为单位向量，求x的值；

（ii）设f（x）=·，则函数y=f（x）的图象是由y=sinx的图象如何平移得到？（变式：研究性质）

（2）已知,且.

（i）求 及;　 （ii）求函数的最小值.

练11 已知向量

（i）求的值； （ii）若的值.

12、向量与三角的应用模型

要求：掌握向量在物理、几何中的应用. 掌握三角模型在实践中的运用.

例12 （1）已知平行四边形，＝，.

（i）若向量与的夹角为60°，，，求，的长.

（ii）如果，求证四边形ABCD为矩形.

（2）某港口水深y（米）是时间t（0≤t≤24，单位：小时）函数，记为y=，下面是某日水深数据：

t（时）	0	3	6	9	12	15	18	21	24
y（米）	10.0	13.0	9.9	7.0	10.0	13.0	10.1	7.0	10.0

经过长期观察，y=的曲线可以近似看成y=Asint+b的图象.

（i）根据以上数据求出y=的近似表达式；

（ii）船底离海底5米或者5米以上是安全的，某船的吃水深度为6.5米（船底离水面距离），如果此船在凌晨4点进港，希望在同一天安全出港，那么此船最多在港口停留多少时间？（忽略进出时间）.

练12 （1）一艘船从点出发以的速度向垂直于对岸的方向行驶，同时河水的流速为，求船实际航行速度的大小为　　　　 ，其方向与水流方向的夹角为　　　　  .

（2）已知的三个顶点的坐标分别为、、，则顶点的坐标为　　　　　　　　 .

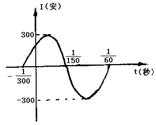
（3）如图，表示电流强度I与时间t的关系式在一个周期内的图象.根据图象得到的一个解析式是　　　　　　  .

（4）已知某海滨浴场的海浪高度y（米）是时间t（0≤t≤24，单位：小时）的函数，经过长期的观察，该函数的图象可以近似地看成. 下表是测得的某日各时的浪高数据：

t(时)	0	3	6	9	12	15	18	21	24
y（米）	1.5	1.0	0.5	1.0	1.5	1.0	0.5	0.99	1.5

依规定，当浪高不低于1米时浴场才开放，试安排白天内开放浴场的具体时间段.

高中新课标数学必修③模块 基础题型归类

1、算法框图与语句：

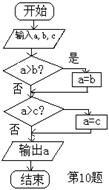
要求：理解算法基本思想，掌握算法三种逻辑结构与五种基本语句（输入、输出、赋值、条件、循环）.

例1. （1）若输入8时，则右边程序执行后输出的结果是　　　　　　 .

（2）右图给出一个算法的程序框图，该程序框图的功能是　　　　　　　　　　　　　　  .

（3）对任意正整数，设计一个求Ｓ＝的程序框图，并编写出程序.

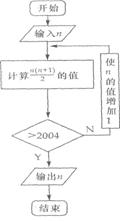
练1 （1）右边程序为一个求20个数的平均数的程序,在横线上应填充的语句为　　　　　 .

（2）右图输出的是的结果是　　　　　  .

（3）编写程序，计算1²+2²+3²+……+100²

2、经典算法案例：

要求：掌握进位制转化、辗转相除法与更相减损术求最大公约数、秦九韶算法.

例2. （1）将二进制数10101_（2）化为十进制数为　　　，再化为八进制数为　　　 .

（2）用辗转相除法求80和36的最大公约数，并用更相减损术检验所得结果.

（3）已知一个4次多项式, 试用秦九韶算法求这个多项式在x=2的值.

练2 （1）下列各数中最小的数是（　　）.　 A. 　 B. 　 C. 　 D.

（2）_（2）= 　　　 _（10），318_（10）= 　　　 _（5）

3、抽样方法与频率分布：

要求：掌握简单随机抽样、系统抽样、分层抽样. 能运用频率分布直方图.

例3. （1）某校1000名学生中，O型血有400人，A型血有250人，B型血有250人，AB型血有100人，为了研究血型与血弱的关系，要从中抽取一个容量为40的样本，按照分层抽样的方法抽取样本，则O型血，A型血，B型血，AB型血的人要分别抽取人数为　　　　　　　　　　  .

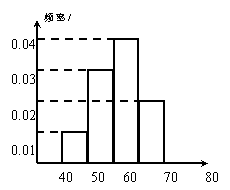（2） 200辆汽车通过某一段公路时的时速频率分布直方图如图所示，则时速在的汽车大约有____________辆

练3 （1）某单位有技工18人、技术员12人、工程师6人，需要从这些人中抽取一个容量为n的样本；如果采用系统抽样和分层抽样方法抽取，都不用剔除个体；如果容量增加一个，则在采用系统抽样时，需要在总体中剔除1个个体，则样本容量n为 　　　　.

（2）某公司生产三种型号的轿车, 产量分别为1200辆,6000辆和2000辆, 为检验该公司的产品质量, 现用分层抽样的方法抽取46辆进行检验, 这三种型号的轿车依次应抽取　　　 辆.

4、样本数字特征：

要求：掌握样本中心位置特征数（平均数、中位数、众数）与离散程度特征数（标准差、方差）的计算.

例4. 给出下列四种说法：

　　① 3，3，4，4，5，5，5的众数是5；

　　② 3，3，4，4，5，5，5的中位数是4.5；

　　③ 频率分布直方图中每一个小长方形的面积等于该组的频率；

　　④ 频率分布表中各小组的频数之和等于1

　其中说法正确的序号依次是　　　　　　　　　 .

练4甲乙两种棉花苗中各抽10株, 测得它们的株高分别如下(单位:cm)

　 甲: 25,41,40,37,22,14,19,39,21,42　  乙: 27,16,44,27,44,16,40,40,16,40

（1）估计两种棉花苗总体的长势:哪种长的高一些?　（2）哪种棉花的苗长得整齐一些?

5、概率基本性质：

要求：掌握概率基本性质等，能运用互斥事件的概率加法公式，对立事件的概率减法公式.

例5. 一枚五分硬币连掷三次，事件A为“三次反面向上”，事件B为“恰有一次正面向上”，事件C为“至少二次正面向上”. 写出一个事件A、B、C的概率之间的正确关系式是　　　　　　　　　　　　　 .

练5 甲、乙两人下棋，甲获胜的概率为30%，甲不输的概率为80%，则甲、乙下成和棋的概率为　　　　；乙获胜的概率为　　　　 .

6、古典概型与几何概型

要求：掌握两种概率模型的特征，能运用概率模型解决实际问题.

例6. （1）玻璃球盒中装有各色球12只，其中5红、4黑、2白、1绿. （i）从中取1个球, 求取得红或白的概率. （ii）若从中取2个球，求至少一个红球的概率.

（2）甲乙两人相约某天在某地点见面，甲计划在上午8：30至9：30之间到达，乙计划在上午9：00至10：00之间到达. （i）求甲比乙提前到达的概率； （ii）如果其中一人先到达后最多等候另一人15分钟，然后离去. 求两人能够会面的概率.

练6 （1）某人一次掷出两枚骰子,点数和为5的概率是　　　.

（2）将一个各个面上均涂有颜色的正方体锯成64个同样大小的正方体，从这些小正方体中任取一个，其中恰有两面涂色的概率是　　　 .

（3）从一副扑克牌（没有大小王）的52张牌中任取2张，求：

（i）2张是不同花色牌的概率； （iii）至少有一张是红心的概率.

（4）在10件产品中，有8件是合格的，2件是次品，从中任意抽2件进行检验，计算：（i）两件都是次品的概率；（ii）2件中恰好有一件是合格品的概率；（iii）至多有一件是合格品的概率

（5）若以连续掷两次骰子分别得到的点数m、n作为点P的坐标，则点P在圆外的概率是　　　　　 .

（6）两人相约7点到8点在某地会面，先到者等候另一人20分钟，过时离去．求两人会面的概率.