第二十三教时
教材：复习二——实数与向量的数量积（续）
目的：继续复习有关知识，提高学生数形结合、解决实际问题的能力。
过程：
一、
继续复习实数与向量的积、向量共线的充要条件、平面向量的基本定理——平几问题
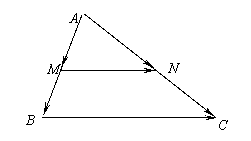
1．如图：已知MN是△ABC的中位线，
求证：MN=
BC, 且MN∥BC
证：∵MN是△ABC的中位线，
∴
, 
∴
∴MN=BC, 且MN∥BC
2．证明：三角形重心与顶点的距离等于它到对边中点的距离的两倍。
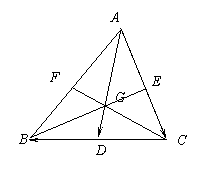证：设
= b，
= a，则
=+
= b+a, 
=
∵A, G, D共线，B, G, E共线
∴可设
=λ，
= μ
,
则=λ=λ(b+a)=λb+λa,
= μ= μ(b+a)=μb+μa,
∵
即：b + (μb+μa) =λb+λa
∴(μ-λ)a + (μ-λ+)b = 0 ∵a, b不平行，
∴
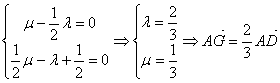
即：AG = 2GD 同理可化：AG = 2GD , CG = 2GF
3．设
=
(a+5b)，
=-2a
+ 8b，=3(a -b)，求证：A,B,D三点共线。
证：=++=(a+5b) + ( -2a
+ 8b)
+ 3(a
-b)
= (1+)a + (5 + 5)b = (1+)(a + 5b)
而=(a+5b)
∴= (
+ 1)
又∵, 有公共点 ∴A,B,D三点共线
4．求证：起点相同的三个非零向量a、b、3a -2b的终点在同一直线上。
证：依题意，可设
= a, 
= b, 
= 3a -2b
=-= b - a
, =-= 3a -2b - a = 2(a
- b)
∴= -2 由于,起点均为A，∴三点A,B,C共线，
即起点相同的三个非零向量a、b、3a -2b的终点在同一直线上
5．已知：平面上三点O、A、B不共线，求证：平面上任一点C与A、B共线的充要条件是存在实数λ和μ，使=λ+ μ，且λ+ μ = 1。
证：必要性：设A,B,C三点共线，则可设= t (tÎR)
则=+=+ t=+ t(-) = (1-t)+ t
令1-t =λ，t = μ，则有：=λ+ μ，且λ+ μ = 1
充分性：=-=λ+ μ-= (λ-1)+ μ
= -μ+ μ= μ(-) = μ
∴三点A、B、C共线
6．某人骑车以每小时a公里的速度向东行驶，感到风从正东方向吹来，而当速度为2a时，感到风从东北方向吹来，试求实际风速和方向。
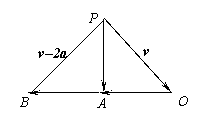解：设a表示此人以每小时a公里的速度向东行驶的向量，
无风时此人感到风速为-a，
设实际风速为v，
那么此时人感到的风速为v - a，
设= -a，= -2a
∵
+=
∴= v - a，这就是感到由正北方向吹来的风速，
∵+=
∴= v -2a，于是当此人的速度是原来的2倍时所感受到由东北方向吹来的风速就是，
由题意：ÐPBO = 45°, PA^BO, BA = AO
从而，△POB为等腰直角三角形，∴PO = PB =a 即：v =a
∴实际风速是a的西北风
二、 作业： 《导学•创新》 §5.3